练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    2．若三个实数成等比数列，第一个数与第三个数的积为4，三个数的和为3，求这三个数．

    分析 设此三个数分别为：$\frac{a}{q}$，a，aq．由题意可得：$\frac{a}{q}$•aq=4，$\frac{a}{q}$+a+aq=3．联立解出即可得出．

    解答 解：设此三个数分别为：$\frac{a}{q}$，a，aq．
    由题意可得：$\frac{a}{q}$•aq=4，$\frac{a}{q}$+a+aq=3．
    联立解得：$\left\{\begin{array}{l}{a=-2}\\{q=-2}\end{array}\right.$或$\left\{\begin{array}{l}{a=-2}\\{q=-\frac{1}{2}}\end{array}\right.$．
    ∴这三个数分别为：1，-2，4；或4，-2，1．

    点评 本题考查了等比数列的通项公式及其性质，考查了推理能力与计算能力，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    12．使等式$\sqrt{\frac{1+sin2θ}{1-sin2θ}}$=$\frac{1}{cos2θ}$+tan2θ成立的角θ的范围是$（-\frac{π}{4}+kπ，\frac{π}{4}+kπ）（k∈Z）$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．已知函数y=loga（x-1）+3，（a＞0且a≠1）的图象恒过点P，则P的坐标是（2，3），若角α的终边经过点P，则sin2α-sin2α的值等于$-\frac{3}{13}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．直线l：x+my-1=0（m∈R）是圆C：x2+y2-4x-2y+1=0的对称轴，若过点A（-4，m）作圆C的一条切线，切点为B，则|AB|=（　　）
    A．2B．4$\sqrt{2}$C．6D．2$\sqrt{10}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

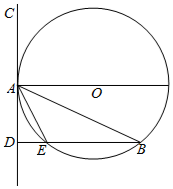    17．如图，在⊙O中，AB是弦，AC是⊙O的切线，A是切点，过B点作BD⊥AC于D，BD交⊙O于E点，若AE平分∠BAD，则∠BAD=60°．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．已知各项均为正数的数列{an}的前n项和满足Sn＞1，6Sn=（an+1）（an+2）．
    （1）求a1的值；
    （2）求数列{an}的通项公式；
    （3）求证：$\frac{1}{{a}_{1}{a}_{2}}$+$\frac{1}{{a}_{2}{a}_{3}}$+…+$\frac{1}{{a}_{n}{a}_{n+1}}$＜$\frac{1}{6}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．如图，在四棱锥P-ABCD中，PD⊥平面ABCD，底面ABCD是菱形，∠BAD=60°，AB=2，PD=2$\sqrt{3}$，O为AC与BD的交点，E为棱PB的中点．
    （Ⅰ）证明：△EAC是等腰直角三角形；
    （Ⅱ）求二面角A-CD-E的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．在四棱锥P-ABCD中，底面ABCD是直角梯形，AD∥BC，AB⊥BC，侧面PAB⊥底面ABCD．若PA=AD=AB=kBC（0＜k＜1），则（　　）
    A．当k=$\frac{1}{2}$时，平面BPC⊥平面PCD
    B．当k=$\frac{1}{2}$时，平面APD⊥平面PCD
    C．对?k∈（0，1），直线PA与底面ABCD都不垂直
    D．?k∈（0，1），使直线PD与直线AC垂直．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．已知m，n∈R+，f（x）=|x+m|+|2x-n|．
    （1）当m=n=1时，求f（x）的最小值；
    （2）若f（x）的最小值为2，求证：$\frac{1}{m}$+$\frac{2}{n}$≥2．

    查看答案和解析>>

    同步练习册答案