
分析 (Ⅰ)直接利用向量的数量积以及二倍角公式两角和的正弦函数化简函数表达式,求出函数的周期,即可求f(x)的解析式.
(Ⅱ)由tanα=2,得到正弦与余弦值,由此得到解析式的值.
(Ⅲ)通过$x∈[\frac{π}{6},\frac{π}{3}]$,求出相位的范围,确定函数的值域,然后利用|f(x)-m|<2,得到m的关系式,求实数m的取值范围.
解答 解:(Ⅰ)∵f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$=2sinωxcosωx+$2\sqrt{3}$cos2ωx,
=sin2ωx+$\sqrt{3}$(1+cos2ωx)=2sin(2ωx+$\frac{π}{3}$)+$\sqrt{3}$
∵相邻两对称轴间的距离为π.∴ω=$\frac{1}{2}$,
∴f(x)=2sin(x+$\frac{π}{3}$)+$\sqrt{3}$.
(Ⅱ)∵tanα=f(0)+2-2$\sqrt{3}$=2,
|sinα|=$\frac{2}{\sqrt{5}}$,|cosα|=$\frac{1}{\sqrt{5}}$,且正弦值域余弦值符号相同.
∴sin2α+sinαcosα+1=$\frac{11}{5}$.
(Ⅲ)∵$x∈[\frac{π}{6},\frac{π}{3}]$,∴x+$\frac{π}{3}$∈[$\frac{π}{2}$,$\frac{2π}{3}$],
∴2$\sqrt{3}$≤f(x)≤2+$\sqrt{3}$
∵|f(x)-m|<2.
∴-2+m<f(x)<2+m,
若对任意实数$x∈[\frac{π}{6},\frac{π}{3}]$,恒有|f(x)-m|<2成立,
则有$\left\{\begin{array}{l}{-2+m≤2\sqrt{3}}\\{2+m≥2+\sqrt{3}}\end{array}\right.$
解得$\sqrt{3}$≤m≤4+2$\sqrt{3}$.
点评 本题考查向量的数量积,两角和与差的三角函数二倍角公式的应用,函数恒成立问题的应用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若四边形不是菱形,则它的两条对角线不垂直 | |
| B. | 若四边形的两条对角线垂直,则它是菱形 | |
| C. | 若四边形的两条对角线垂直,则它不是菱形 | |
| D. | 若四边形是菱形,则它的两条对角线垂直 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
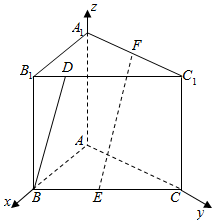 在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1=2,E、F分别是BC,A1C1的中点.
在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1=2,E、F分别是BC,A1C1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com