
| A. | ${\overrightarrow e_1}$和 ${\overrightarrow e_1}$+${\overrightarrow e_2}$ | B. | ${\overrightarrow e_1}$-2${\overrightarrow e_2}$和${\overrightarrow e_1}$-${\overrightarrow e_2}$ | ||
| C. | ${\overrightarrow e_1}$+${\overrightarrow e_2}$和${\overrightarrow e_1}$-${\overrightarrow e_2}$ | D. | 2${\overrightarrow e_1}$-${\overrightarrow e_2}$和$\frac{1}{2}$${\overrightarrow e_2}$-${\overrightarrow e_1}$ |
分析 判断各组所给的两个向量是否共线得出答案.
解答 解:∵2$\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{2}}$=-2($\frac{1}{2}\overrightarrow{{e}_{2}}$-$\overrightarrow{{e}_{1}}$),故2$\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{2}}$与$\frac{1}{2}\overrightarrow{{e}_{2}}$-$\overrightarrow{{e}_{1}}$共线,
∴2$\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{2}}$和$\frac{1}{2}\overrightarrow{{e}_{2}}$-$\overrightarrow{{e}_{1}}$不能作为平面向量的一组基底.,
故选:D.
点评 本题考查了平面向量的基本定理,属于基础题.


科目:高中数学 来源: 题型:选择题
 若用P表示已知条件、已有的定义、定理、公理等,Q表示所要证明的结论,则如图框图表示的证明方法是( )
若用P表示已知条件、已有的定义、定理、公理等,Q表示所要证明的结论,则如图框图表示的证明方法是( )| A. | 合情推理 | B. | 综合法 | C. | 分析法 | D. | 反证法 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 2$\sqrt{3}$ | C. | $\frac{7\sqrt{2}}{3}$ | D. | $\frac{7\sqrt{2}}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\sqrt{2}$,+∞) | B. | (1,$\sqrt{2}$] | C. | (1,$\sqrt{3}$) | D. | ($\sqrt{2}$,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (-1,0) | C. | (0,$\sqrt{2}$) | D. | (-$\sqrt{2}$,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
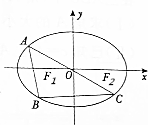 已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右两个焦点F1,F2,过其中两个端点的直线斜率为$\frac{\sqrt{2}}{2}$,过两个焦点和一个顶点的三角形面积为1.
已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右两个焦点F1,F2,过其中两个端点的直线斜率为$\frac{\sqrt{2}}{2}$,过两个焦点和一个顶点的三角形面积为1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com