练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    17．若用P表示已知条件、已有的定义、定理、公理等，Q表示所要证明的结论，则如图框图表示的证明方法是（　　）
    A．合情推理B．综合法C．分析法D．反证法

    分析 根据证题思路，是由因导果，是综合法的思路，故可得结论．

    解答 解：∵P表示已知条件或已有的定义、公理或定理，Q表示所得到的结论，
    ∴证明方法是由因导果，是综合法的思路
    故选：B

    点评 本题主要考查综合法的思路：由因导果，比较简单，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    2．已知x-y=2，求x3-6xy-y3的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

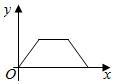    8．如图所示是南京青奥会传递火炬时，火炬离主会场距离（y）与传递时间（x）之间的函数关系的图象，若用黑点表示主会场的位置，则火炬传递的路线可能是（　　）
    A．B．C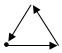．D．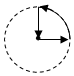

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．教材曾有介绍：圆x2+y2=r2上的点（x0，y0）处的切线方程为x${\;}_{0}x+{y}_{0}y={r}^{2}$，我们将其结论推广：椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）上的点（x0，y0）处的切线方程为$\frac{{x}_{0}x}{{a}^{2}}+\frac{{y}_{0}y}{{b}^{2}}=1$，在解本题时可以直接应用，已知：直线x-y+$\sqrt{3}$=0与椭圆E：$\frac{{x}^{2}}{{a}^{2}}+{y}^{2}$=1（a＞1）有且只有一个公共点；
    （1）求a的值；
    （2）设O为坐标原点，过椭圆E上的两点A、B分别作该椭圆的两条切线l1、l2，且l1与l2交于点M（2，m），当m变化时，求△OAB面积的最大值；
    （3）在（2）的条件下，经过点M（2，m）作直线l与该椭圆E交于C、D两点，在线段CD上存在点N，使$\frac{|CN|}{|ND|}=\frac{|MC|}{|MD|}$成立，试问：点N是否在直线AB上，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．图是一个商场某段时间制定销售计划时的局部结构图，从图中可以看出“计划”的制定主要受（　　）个因素的影响．
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．已知函数f（x）=x+alnx，g（x）=f（x）+$\frac{1}{2}{x^2}$-bx．
    （1）讨论函数f（x）的单调性；
    （2）若f（x）在x=1处的切线与直线x+2y=0垂直，求a的值；
    （3）在（2）的条件下，设x1，x2（x1＜x2）是函数g（x）的两个极值点，记t=$\frac{x_1}{x_2}$，若b≥$\frac{13}{3}$，t的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．“如果b⇒c，a⇒b，则a⇒c”这种推理规则叫做演绎推理．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）过点P（1，$\frac{3}{2}$），其离心率为$\frac{1}{2}$．
    （1）求椭圆C的方程；
    （2）设椭圆C的右顶点为A，直线l交C于两点M、N（异于点A），且AM⊥AN，证明直线l过定点．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．已知${\overrightarrow e_1}$和${\overrightarrow e_2}$是表示平面内所有向量的一组基底，那么下面四组向量中不能作为一组基底的是（　　）
    A．${\overrightarrow e_1}$和 ${\overrightarrow e_1}$+${\overrightarrow e_2}$B．${\overrightarrow e_1}$-2${\overrightarrow e_2}$和${\overrightarrow e_1}$-${\overrightarrow e_2}$
    C．${\overrightarrow e_1}$+${\overrightarrow e_2}$和${\overrightarrow e_1}$-${\overrightarrow e_2}$D．2${\overrightarrow e_1}$-${\overrightarrow e_2}$和$\frac{1}{2}$${\overrightarrow e_2}$-${\overrightarrow e_1}$

    查看答案和解析>>

    同步练习册答案