
 :
:
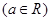 .若存在实数
.若存在实数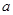 使得一条曲线与直线
使得一条曲线与直线 有两个不同的交点,且以这两个交点为端点的线段长度恰好等于
有两个不同的交点,且以这两个交点为端点的线段长度恰好等于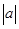 ,则称此曲线为直线
,则称此曲线为直线 的“绝对曲线”.下面给出四条曲线方程:①
的“绝对曲线”.下面给出四条曲线方程:①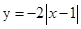 ;②
;②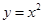 ;③
;③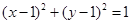 ;④
;④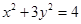 ;则其中直线
;则其中直线 的“绝对曲线”有 ( )
的“绝对曲线”有 ( )| A.①④ | B.②③ | C.②④ | D.②③④ |
 表示斜率为
表示斜率为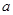 且过定点(1,1)的直线.(1)曲线①是由左右两支射线构成:
且过定点(1,1)的直线.(1)曲线①是由左右两支射线构成: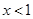 时,是斜率为2且过点(1,0)的射线;
时,是斜率为2且过点(1,0)的射线;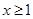 时,是斜率为-2且过点(1,0)的射线.作图可知:当
时,是斜率为-2且过点(1,0)的射线.作图可知:当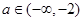 ,直线
,直线 仅与曲线①右支射线有一个交点;当
仅与曲线①右支射线有一个交点;当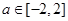 时,直线
时,直线 与曲线①无交点;当
与曲线①无交点;当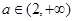 时,直线
时,直线 仅与曲线①左支射线有一个交点.所以直线
仅与曲线①左支射线有一个交点.所以直线 与曲线①最多只有一个交点,不符题意,故曲线①不是直线
与曲线①最多只有一个交点,不符题意,故曲线①不是直线 的“绝对曲线”.(2)因为定点(1,1)在曲线②上,所以直线
的“绝对曲线”.(2)因为定点(1,1)在曲线②上,所以直线 与曲线②恒有交点,设曲线②与直线
与曲线②恒有交点,设曲线②与直线 的两交点为
的两交点为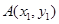 、
、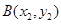 ,易知
,易知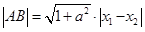
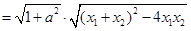 ,联立直线
,联立直线 与曲线②方程,化简得:
与曲线②方程,化简得: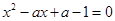 .
.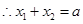
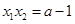 .
.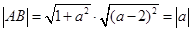 ,从而可知当且仅当
,从而可知当且仅当 时直线
时直线 与曲线②仅一个交点.两边平方,化简得:
与曲线②仅一个交点.两边平方,化简得: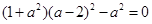 .设
.设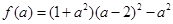 ,则
,则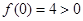 ,
,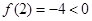 ,且
,且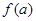 是连续函数,所以
是连续函数,所以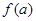 在(0,2)上有零点,即方程
在(0,2)上有零点,即方程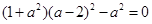 在(0,2)上有根,且在(0,2)上曲线②与直线
在(0,2)上有根,且在(0,2)上曲线②与直线 有两个不同的交点.故存在实数
有两个不同的交点.故存在实数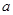 使得曲线②与直线
使得曲线②与直线 两个不同交点为端点的线段长度恰好等于
两个不同交点为端点的线段长度恰好等于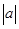 ,故曲线②是直线
,故曲线②是直线 的“绝对曲线”.(3)曲线③表示圆心在(1,1)且半径为1的圆,它与直线
的“绝对曲线”.(3)曲线③表示圆心在(1,1)且半径为1的圆,它与直线 两个交点为端点的线段长度恒为2,
两个交点为端点的线段长度恒为2,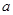 为2或-2时满足题意,故曲线③是直线
为2或-2时满足题意,故曲线③是直线 的“绝对曲线”.(4)因为定点(1,1)在曲线④上,所以直线
的“绝对曲线”.(4)因为定点(1,1)在曲线④上,所以直线 与曲线④恒有交点,设曲线④与直线
与曲线④恒有交点,设曲线④与直线 的两交点为
的两交点为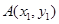 、
、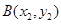 ,易知
,易知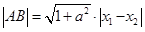
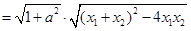 ,联立直线
,联立直线 与曲线④方程,化简得:
与曲线④方程,化简得: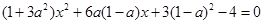
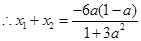 ,
,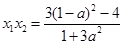 ,
,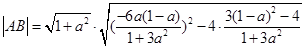
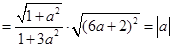 ,从而可知当且仅当
,从而可知当且仅当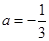 时直线
时直线 与曲线④仅一个交点.两边平方,化简得:
与曲线④仅一个交点.两边平方,化简得: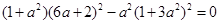 .
.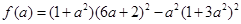 ,
,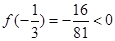 ,
,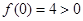 ,且
,且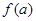 是连续函数,所以
是连续函数,所以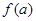 在
在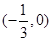 上有零点,即方程
上有零点,即方程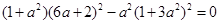 在
在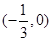 上有根,且在
上有根,且在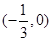 上曲线④与直线
上曲线④与直线 有两个不同的交点.故存在实数
有两个不同的交点.故存在实数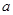 使得曲线④与直线
使得曲线④与直线 两个交点为端点的线段长度恰好等于
两个交点为端点的线段长度恰好等于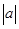 ,故曲线④是直线
,故曲线④是直线 的“绝对曲线”.
的“绝对曲线”.

科目:高中数学 来源:不详 题型:解答题
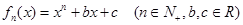
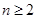 ,
,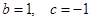 ,证明:
,证明: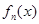 在区间
在区间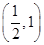 内存在唯一的零点;
内存在唯一的零点;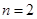 ,若对任意
,若对任意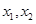
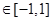 ,有
,有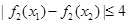 ,求
,求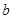 的取值范围;
的取值范围;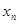 是
是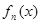 在
在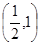 内的零点,判断数列
内的零点,判断数列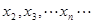 的增减性.
的增减性.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
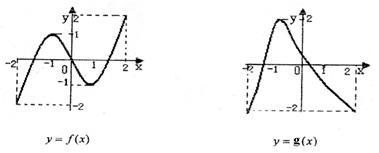
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.3 | B.4 | C.5 | D.6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com