
已知双曲线![]() 的中心在坐标原点,渐近线方程是
的中心在坐标原点,渐近线方程是![]() ,左焦点的坐标为
,左焦点的坐标为![]() ,
,![]() 为双曲线
为双曲线![]() 上的两个动点,满足
上的两个动点,满足![]() .
.
(Ⅰ)求双曲线![]() 的方程;
的方程;
(Ⅱ)求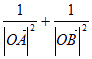 的值;
的值;
(Ⅲ)动点![]() 在线段
在线段![]() 上,满足
上,满足![]() ,求证:点
,求证:点![]() 在定圆上.
在定圆上.
(Ⅰ) ![]() (Ⅱ)
(Ⅱ) 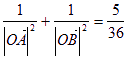 (Ⅲ)见解析
(Ⅲ)见解析
(Ⅰ)由题意,设双曲线C的方程为![]()
![]() ,则由
,则由![]() 得
得![]()
所以双曲线![]() 的方程为
的方程为![]() ………………………………2分
………………………………2分
(Ⅱ)解法一:①当过![]() 两点的直线斜率存在时,设直线
两点的直线斜率存在时,设直线![]() 的方程为
的方程为![]() ,则
,则
由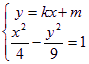 得
得![]() ……………………4分
……………………4分
设![]() 则
则![]()
∴![]() …………5分
…………5分
又![]() ,则
,则![]()
即![]()
∴![]()
满足△![]() ……………………………6分
……………………………6分
设原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
则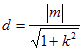 ,又由
,又由![]()
∴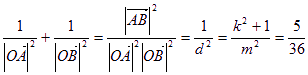
![]()
∴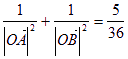 为定值……………………………………8分
为定值……………………………………8分
②当过![]() 两点的直线斜率不存在时, 设直线
两点的直线斜率不存在时, 设直线![]() 的方程为
的方程为![]() ,则可验证
,则可验证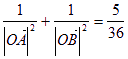 为定值…………………………………………10分
为定值…………………………………………10分
解法二:设![]() ,则
,则![]() ……………6分
……………6分
点![]() 在双曲线上,则
在双曲线上,则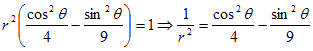
由![]() 得
得![]()
同理, ![]() …………………8分
…………………8分
所以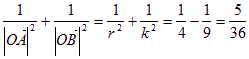 为定值…………………10分
为定值…………………10分
(Ⅲ)由三角形面积公式,得![]()
所以![]()
即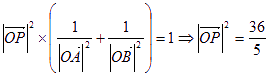
所以点![]() 在以原点为圆心,
在以原点为圆心,![]() 半径的圆上……………………13分
半径的圆上……………………13分


科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com