
【题目】已知函数f(x)=m6x﹣4x , m∈R.
(1)当m= ![]() 时,求满足f(x+1)>f(x)的实数x的范围;
时,求满足f(x+1)>f(x)的实数x的范围;
(2)若f(x)≤9x对任意的x∈R恒成立,求实数m的范围.
【答案】
(1)解:当m= ![]() 时,f(x+1)>f(x)
时,f(x+1)>f(x)
即为 ![]() 6x+1﹣4x+1>
6x+1﹣4x+1> ![]() 6x﹣4x,
6x﹣4x,
化简得,( ![]() )x<
)x< ![]() ,
,
解得x>2.
则满足条件的x的范围是(2,+∞)
(2)解:f(x)≤9x对任意的x∈R恒成立即为m6x﹣4x≤9x,
即m≤ ![]() =(
=( ![]() )﹣x+(
)﹣x+( ![]() )x对任意的x∈R恒成立,
)x对任意的x∈R恒成立,
由于( ![]() )﹣x+(
)﹣x+( ![]() )x≥2,当且仅当x=0取最小值2.
)x≥2,当且仅当x=0取最小值2.
则m≤2.
故实数m的范围是(﹣∞,2]
【解析】(1)当m= ![]() 时,f(x+1)>f(x)即可化简得,(
时,f(x+1)>f(x)即可化简得,( ![]() )x<
)x< ![]() ,由单调性即可得到;(2)f(x)≤9x对任意的x∈R恒成立即m≤
,由单调性即可得到;(2)f(x)≤9x对任意的x∈R恒成立即m≤ ![]() =(
=( ![]() )﹣x+(
)﹣x+( ![]() )x对任意的x∈R恒成立,运用基本不等式即可得到最小值,令m不大于最小值即可.
)x对任意的x∈R恒成立,运用基本不等式即可得到最小值,令m不大于最小值即可.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】《聊斋志异》中有这样一首诗:“挑水砍柴不堪苦,请归但求穿墙术.得诀自诩无所阻,额上坟起终不悟.”在这里,我们称形如以下形式的等式具有“穿墙术”: 2 ![]() =
= ![]() ,3
,3 ![]() =
= ![]() ,4
,4 ![]() =
= ![]() ,5
,5 ![]() =
= ![]()
则按照以上规律,若8 ![]() =
= ![]() 具有“穿墙术”,则n=( )
具有“穿墙术”,则n=( )
A.7
B.35
C.48
D.63
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲和乙参加有奖竞猜闯关活动,活动规则:①闯关过程中,若闯关成功则继续答题;若没通关则被淘汰;②每人最多闯3关;③闯第一关得10万奖金,闯第二关得20万奖金,闯第三关得30万奖金,一关都没过则没有奖金.已知甲每次闯关成功的概率为 ![]() ,乙每次闯关成功的概率为
,乙每次闯关成功的概率为 ![]() .
.
(1)设乙的奖金为ξ,求ξ的分布列和数学期望;
(2)求甲恰好比乙多30万元奖金的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)=ax2+bx(a,b为常数,且a≠0)满足条件:f(x﹣1)=f(3﹣x)且方程f(x)=2x有两个相等实数根 (Ⅰ)求f(x)的解析式;
(Ⅱ)是否存在实数m,n(m<n),使f(x)的定义域和值域分别为[m,n]和[4m,4n],如果存在,求出符合条件的所有m,n的值,如果不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() sin2x﹣cos2x+1,下列结论中错误的是( )
sin2x﹣cos2x+1,下列结论中错误的是( )
A.f(x)的图象关于( ![]() ,1)中心对称
,1)中心对称
B.f(x)在( ![]() ,
, ![]() )上单调递减
)上单调递减
C.f(x)的图象关于x= ![]() 对称
对称
D.f(x)的最大值为3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设全集U=R,集合M={x||x﹣ ![]() |
| ![]() },P={x|﹣1≤x≤4},则(UM)∩P等于( )
},P={x|﹣1≤x≤4},则(UM)∩P等于( )
A.{x|﹣4≤x≤﹣2}
B.{x|﹣1≤x≤3}
C.{x|3<x≤4}
D.{x|3≤x≤4}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=3x的定义域为R,满足f(a+2)=18,函数g(x)=λ3ax﹣4x的定义域为[0,1].
(1)求实数a的值;
(2)若函数g(x)为定义域上单调减函数,求实数λ的取值范围;
(3)λ为何值时,函数g(x)的最大值为 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标平面内,以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程是ρ=4sinθ,直线l的参数方程是 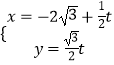 (t为参数).
(t为参数).
(1)求直线l的普通方程和曲线C的直角坐标方程;
(2)求曲线C上的点到直线l的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着智能手机的发展,微信越来越成为人们交流的一种方式.某机构对使用微信交流的态度进行调查,随机调查了 50 人,他们年龄的频数分布及对使用微信交流赞成人数如表.
年龄(岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 5 | 10 | 12 | 7 | 2 | 1 |
(I)由以上统计数据填写下面 2×2 列联表,并判断是否有99%的把握认为年龄45岁为分界点对使用微信交流的态度有差异;
年龄不低于45岁的人 | 年龄低于45岁的人 | 合计 | |
赞成 | |||
不赞成 | |||
合计 |
(Ⅱ)若对年龄在[55,65),[65,75)的被调查人中随机抽取两人进行追踪调查,记选中的4人中赞成使用微信交流的人数为X,求随机变量X的分布列和数学期望
参考公式:K2= ![]() ,其中n=a+b+c+d
,其中n=a+b+c+d
参考数据:
P(K2≥k0) | 0.050 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com