
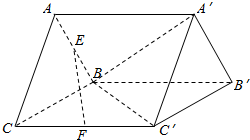
 已知三棱柱ABC-A′B′C′如图所示,四边形BCC′B′为菱形,∠BCC′=60°,△ABC为等边三角形,面ABC⊥面BCC′B′,E、F分别为棱AB、CC′的中点.
已知三棱柱ABC-A′B′C′如图所示,四边形BCC′B′为菱形,∠BCC′=60°,△ABC为等边三角形,面ABC⊥面BCC′B′,E、F分别为棱AB、CC′的中点.分析 (Ⅰ)(法一)取A'B中点D,连接ED,DC,推导出四边形EFCD为平行四边形,从而EF∥CD,由引能证明EF∥面A'BC.
(法二)取AA'中点G,连接EG,FG,则EG∥A'B,FG∥A'C',从而面EFG∥面A'BC',由此能证明EF∥面A'BC.
(法三)取BC中点O,连接AO,OC',建立空间直角坐标系,利用向量法能证明EF∥面A'BC.
(Ⅱ)(法一)过F点作AA'的垂线FM交AA'于M,连接BM,BF,则∠BMF为二面角C-AA'-B的平面角,由此能求出二面角C-AA'-B的大小.
(法二)利用向量法能求出二面角C-AA'-B的大小.
解答  证明:(Ⅰ)(方法一)取A'B中点D,连接ED,DC,
证明:(Ⅰ)(方法一)取A'B中点D,连接ED,DC,
因为E,D分别为AB,A'B中点,
所以$ED=\frac{1}{2}AA',ED∥AA'$,(3分)
所以ED=CF,ED∥CF,所以四边形EFCD为平行四边形,所以EF∥CD,又因为EF?面A'BC,CD?面A'BC,所以EF∥面A'BC.(6分)
(方法二)取AA'中点G,连接EG,FG,
因为E,G分别为AB,AA'中点,所以EG∥A'B
又因为F,G分别为CC',AA'中点,所以FG∥A'C'(3分)
且EG?面EFG,GF?面EFG,EG∩GF=G,A'C'?面A'BC',A'B?面A'BC',A'C'∩A'B=A',
所以面EFG∥面A'BC',
又EF?面EFG,所以EF∥面A'BC.(6分)
(方法三)取BC中点O,连接AO,OC',
由题可得AO⊥BC,又因为面ABC⊥面BCC'B',
所以AO⊥面BCC'B',又因为菱形BCC'B'中∠BCC'=60°,所以C'O⊥BC.
可以建立如图所示的空间直角坐标系,(7分)
不妨设BC=2,
可得C(1,0,0),$C'(0,\sqrt{3},0)$$A(0,0,\sqrt{3})$,
B(-1,0,0),$A'(-1,\sqrt{3},\sqrt{3})$,$B'(-2,\sqrt{3},0)$,
所以$E(-\frac{1}{2},0,\frac{{\sqrt{3}}}{2}),F(\frac{1}{2},\frac{{\sqrt{3}}}{2},0)$
所以$\overrightarrow{EF}=(1,\frac{{\sqrt{3}}}{2},-\frac{{\sqrt{3}}}{2}),\overrightarrow{BC'}=(1,\sqrt{3},0),\overrightarrow{BA'}=(0,\sqrt{3},\sqrt{3})$,┅┅┅┅┅┅┅(9分)
设面A'BC的一个法向量为$\vec n=(a,b,c)$,
则$\left\{{\begin{array}{l}{a+\sqrt{3}b=0}\\{\sqrt{3}b+\sqrt{3}c=0}\end{array}}\right.$,不妨取$a=\sqrt{3}$,则$(a,b,c)=(\sqrt{3},-1,1)$,
所以$\overrightarrow{EF}•\vec n=0$,又因为EF?面A'BC,所以EF∥面A'BC.(12分)
解:(Ⅱ)(方法一)过F点作AA'的垂线FM交AA'于M,连接BM,BF.
因为BF⊥CC',CC'∥AA',
所以BF⊥AA',所以AA'⊥面MBF,
所以∠BMF为二面角C-AA'-B的平面角.(8分)
因为面ABC⊥面BCC'B',所以A$\left\{{\begin{array}{l}{-{x_1}-\sqrt{3}{z_1}=0}\\{-{x_1}+\sqrt{3}{y_1}=0}\end{array}}\right.$
点在面BCC'B'上的射影落在BC上,
所以$cos∠ACC'=cos∠BCC'cos∠ACB=\frac{1}{4}$,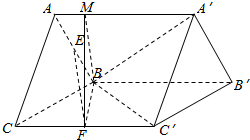
所以$sin∠ACC'=\frac{{\sqrt{15}}}{4}=\frac{MF}{AC}$,
不妨设BC=2,所以$MF=\frac{{\sqrt{15}}}{2}$,同理可得$BM=\frac{{\sqrt{15}}}{2}$.(10分)
所以$cos∠BMF=\frac{{\frac{15}{4}+\frac{15}{4}-3}}{{\frac{15}{2}}}=\frac{3}{5}$,
所以二面角C-AA'-B的大小为$arccos\frac{3}{5}$.(12分)
(方法二)接(Ⅰ)方法三可得$\overrightarrow{AB}=(-1,0,-\sqrt{3}),\overrightarrow{AA'}=(-1,\sqrt{3},0)$,
设面AA'B的一个法向量为${\vec n_1}=({x_1},{y_1},{z_1})$,
则不妨取${x_1}=\sqrt{3}$,则$({x_1},{y_1},{z_1})=(\sqrt{3},1,-1)$.(8分)
又$\overrightarrow{AC}=(1,0,-\sqrt{3}),\overrightarrow{AA'}=(-1,\sqrt{3},0)$,
设面AA'C的一个法向量为${\vec n_2}=({x_2},{y_2},{z_2})$,
则$\left\{{\begin{array}{l}{{x_2}-\sqrt{3}{z_2}=0}\\{-{x_2}+\sqrt{3}{y_2}=0}\end{array}}\right.$,不妨取${x_2}=\sqrt{3}$,则$({x_2},{y_2},{z_2})=(\sqrt{3},1,1)$.(10分)
所以$cos<{\vec n_1},{\vec n_2}>=\frac{{{{\vec n}_1}•{{\vec n}_2}}}{{|{{\vec n}_1}|•|{{\vec n}_2}|}}=\frac{3}{5}$,因为二面角C-AA'-B为锐角,
所以二面角C-AA'-B的大小为┅┅┅┅(12分)
点评 本题考查线面平行的证明,考查二面角的大小的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:高中数学 来源: 题型:选择题
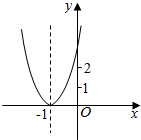 已知二次函数y=ax2+bx+c+2的图象如图所示,顶点为(-1,0),下列结论:①abc<0;②b2-4ac=0;③a>2;④4a-2b+c>0.其中正确结论的个数是( )
已知二次函数y=ax2+bx+c+2的图象如图所示,顶点为(-1,0),下列结论:①abc<0;②b2-4ac=0;③a>2;④4a-2b+c>0.其中正确结论的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a≥-4 | B. | -3<a≤4 | C. | a≥4或a≤-3 | D. | a≥4或a<-3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com