
【题目】写出与下列各角终边相同的角的集合S,并把S中适合不等式-360°≤β<720°的元素β写出来:
(1)60°; (2)-21°.
【答案】(1) 集合S={β|β=![]() +60°,k∈Z} ,β=-300°,β=60°,β=420°.(2) 集合S={β|β=
+60°,k∈Z} ,β=-300°,β=60°,β=420°.(2) 集合S={β|β=![]() -21°,k∈Z},β=-21°, β=339°,β=699°.
-21°,k∈Z},β=-21°, β=339°,β=699°.
【解析】
根据终边相同的角的概念,写出与所求角的终边相同的角的集合S,再求出S中适合条件的元素β即可.
解:(1)60°,终边所在的集合S={β|β=![]() +60°,k∈Z}.
+60°,k∈Z}.
k=-1时,β=-300°;k=0时,β=60°;k=1时,β=420°;
S中适合不等式-360°≤β<720°的元素β为:-300°,60°,420°.
(2)-21°,终边所在的集合S={β|β=![]() -21°,k∈Z}.
-21°,k∈Z}.
k=0时β=-21°,;k=1时,β=339°;k=2时,β=699°.
S中适合不等式-360°≤β<720°的元素β为:-21°,339°,699°.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:高中数学 来源: 题型:
【题目】现有A,B两个投资项目,投资两项目所获得利润分别是![]() 和
和![]() (万元),它们与投入资金
(万元),它们与投入资金![]() (万元)的关系依次是:其中
(万元)的关系依次是:其中![]() 与
与![]() 平方根成正比,且当
平方根成正比,且当![]() 为4(万元)时
为4(万元)时![]() 为1(万元),又
为1(万元),又![]() 与
与![]() 成正比,当
成正比,当![]() 为4(万元)时
为4(万元)时![]() 也是1(万元);某人甲有3万元资金投资.
也是1(万元);某人甲有3万元资金投资.
(Ⅰ)分别求出![]() ,
,![]() 与
与![]() 的函数关系式;
的函数关系式;
(Ⅱ)请帮甲设计一个合理的投资方案,使其获利最大,并求出最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列结论中:
①定义在R上的函数f(x)在区间(-∞,0]上是增函数,在区间[0,+∞)上也是增函数,则函数f(x)在R上是增函数;②若f(2)=f(-2),则函数f(x)不是奇函数;③函数y=x-0.5是(0,1)上的减函数;④对应法则和值域相同的函数的定义域也相同;⑤若x0是二次函数y=f(x)的零点,且m<x0<n,那么f(m)f(n)<0一定成立.
写出上述所有正确结论的序号:_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() ,
,![]() 时,求满足
时,求满足![]() 的
的![]() 的值;
的值;
(2)若函数![]() 是定义在
是定义在![]() 上的奇函数.
上的奇函数.
①存在![]() ,使得不等式
,使得不等式![]() 有解,求实数
有解,求实数![]() 的取值范围;
的取值范围;
②若函数![]() 满足
满足![]() ,若对任意
,若对任意![]() 且
且![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() .
.
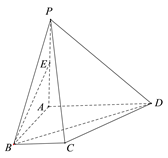
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.
(i)过点![]() 作一直线
作一直线![]() 与
与![]() 平行,在图中画出直线
平行,在图中画出直线![]() 并说明理由;
并说明理由;
(ii)求平面![]() 将三棱锥
将三棱锥![]() 分成的两部分体积的比.
分成的两部分体积的比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学习小组在暑期社会实践活动中,通过对某商店一种商品销售情况的调查发现:该商品在过去的一个月内(以30天计)的日销售价格![]() (元)与时间
(元)与时间![]() (天)的函数关系近似满足
(天)的函数关系近似满足![]() (
(![]() 为正常数).该商品的日销售量
为正常数).该商品的日销售量![]() (个)与时间
(个)与时间![]() (天)部分数据如下表所示:
(天)部分数据如下表所示:
| 10 | 20 | 25 | 30 |
| 110 | 120 | 125 | 120 |
已知第10天该商品的日销售收入为121元.
(I)求![]() 的值;
的值;
(II)给出以下二种函数模型:
①![]() ,②
,②![]() ,
,
请你根据上表中的数据,从中选择你认为最合适的一种函数来描述该商品的日销售量![]() 与时间
与时间![]() 的关系,并求出该函数的解析式;
的关系,并求出该函数的解析式;
(III)求该商品的日销售收入![]() (元)的最小值.
(元)的最小值.
(函数![]() ,在区间
,在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增.性质直接应用.)
上单调递增.性质直接应用.)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com