
 如图,已知A、B是单位圆O上的点,C是圆与x轴正半轴的交点,点A的坐标为(
如图,已知A、B是单位圆O上的点,C是圆与x轴正半轴的交点,点A的坐标为(| 3 |
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| ||
| 2 |
| 4 |
| 5 |
| 1 |
| 2 |
| 3 |
| 5 |
4
| ||
| 10 |
| 1 |
| 2 |
4
| ||
| 10 |
3+4
| ||
| 20 |


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:高中数学 来源: 题型:
| f(x2)-f(x1) |
| x2-x1 |
| f(b)-f(a) |
| b-a |
| b-a |
| b |
| b |
| a |
| b-a |
| a |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
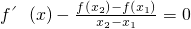 在(x1,x2)恒有实数解
在(x1,x2)恒有实数解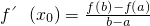 .如我们所学过的指、对数函数,正、余弦函数等都符合拉格朗日中值定理条件.试用拉格朗日中值定理证明:
.如我们所学过的指、对数函数,正、余弦函数等都符合拉格朗日中值定理条件.试用拉格朗日中值定理证明: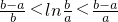 (可不用证明函数的连续性和可导性).
(可不用证明函数的连续性和可导性).查看答案和解析>>
科目:高中数学 来源:2010-2011学年黑龙江省哈尔滨六中高一(上)期末数学试卷(解析版) 题型:选择题


查看答案和解析>>
科目:高中数学 来源:2008-2009学年广东省广州六中高三(上)9月月考数学试卷(理科)(解析版) 题型:解答题
 在(x1,x2)恒有实数解
在(x1,x2)恒有实数解 .如我们所学过的指、对数函数,正、余弦函数等都符合拉格朗日中值定理条件.试用拉格朗日中值定理证明:
.如我们所学过的指、对数函数,正、余弦函数等都符合拉格朗日中值定理条件.试用拉格朗日中值定理证明: (可不用证明函数的连续性和可导性).
(可不用证明函数的连续性和可导性).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com