练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知定义在R上的偶函数f(x)，f(1)＝0，当x>0时有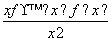>0，则不等式xf(x)>0的解集为(　　)

    A．{x|－1<x<0}                          B．{x|x>1或－1<x<0}

    C．{x|x>0}                              D．{x|－1<x<1}


    B解析　当x>0时有

    即′>0，∴在(0，＋∞)上单调递增．

    ∵f(x)为R上的偶函数，∴xf(x)为R上的奇函数．

    ∵xf(x)>0，∴x2>0.∴>0.

    ∵在(0，＋∞)上单调递增，且＝0，

    ∴当x>0时，若xf(x)>0，则x>1.

    又∵xf(x)为R上的奇函数，∴当x<0时，

    若xf(x)>0，则－1<x<0.

    综上，不等式的解集为{x|x>1或－1<x<0}．

    答案　B


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知函数f(x)＝x3－x2＋＋.

    证明：存在x0∈，使f(x0)＝x0.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数f(x)＝1＋x－sinx在(0,2π)上的单调情况是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知f(x)＝x3－6x2＋9x－abc，a<b<c，且f(a)＝f(b)＝f(c)＝0.现给出如下结论：

    ①f(0)f(1)>0；②f(0)f(1)<0；

    ③f(0)f(3)>0；④f(0)f(3)<0.

    其中正确结论的序号是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知f(x)＝ax－lnx，x∈(0，e]，g(x)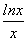＝，其中e是自然常数，a∈R.

    (1)讨论当a＝1时，函数f(x)的单调性和极值；

    (2)求证：在(1)的条件下，f(x)>g(x)＋；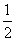

    (3)是否存在实数a，使f(x)的最小值是3？若存在，求出a的值；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某种产品每件成本为6元，每件售价为x元(6<x<11)，年销售为u万件，若已知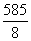－u与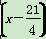2成正比，且售价为10元时，年销量为28万件．

    (1)求年销售利润y关于售价x的函数关系式；

    (2)求售价为多少时，年利润最大，并求出最大年利润．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    一辆汽车在高速公路上行驶，由于遇到紧急情况而刹车，以速度v(t)＝7－3t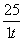＋(t的单位：s，v的单位：m/s)行驶至停止．在此期间汽车继续行驶的距离(单位：m)是(　　)

    A．1＋25ln5                             B．8＋25ln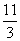

    C．4＋25ln5                             D．4＋50ln2

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知角α的顶点与原点重合，始边与x轴的正半轴重合，终边上一点的坐标为(3,4)，则cos2α＝________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    下列关系式中正确的是(　　)

    A．sin11°<cos10°<sin168°

    B．sin168°<sin11°<cos10°

    C．sin11°<sin168°<cos10°

    D．sin168°<cos10°<sin11°

    查看答案和解析>>

    同步练习册答案