
已知f(x)=ax-lnx,x∈(0,e],g(x)=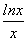 ,其中e是自然常数,a∈R.
,其中e是自然常数,a∈R.
(1)讨论当a=1时,函数f(x)的单调性和极值;
(2)求证:在(1)的条件下,f(x)>g(x)+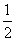 ;
;
(3)是否存在实数a,使f(x)的最小值是3?若存在,求出a的值;若不存在,说明理由.
解 (1)∵f(x)=x-lnx,f′(x)=1-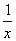 =
= ,
,
∴当0<x<1时,f′(x)<0,f(x)单调递减;
当1<x<e时,f′(x)>0,f(x)单调递增.
∴f(x)的极小值为f(1)=1.
(2)证明:∵f(x)的极小值为1,即f(x)在(0,e]上的最小值为 1,∴f(x)min=1.
又∵g′(x)= ,
,
∴0<x<e时,g′(x)>0,g(x)在(0,e]上单调递增.
∴g(x)max=g(e)= <
<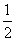 .
.
∴f(x)min-g(x)max>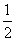 .
.
∴在(1)的条件下,f(x)>g(x)+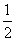 .
.
(3)假设存在实数a,使f(x)=ax-lnx(x∈(0,e])有最小值3,则f′(x)=a-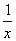 =
= .
.
①当a≤0时,f(x)在(0,e]上单调递减,f(x)min=f(e)=ae-1=3,a= (舍去),所以,此时f(x)的最小值不是3;
(舍去),所以,此时f(x)的最小值不是3;
 ③当
③当 ≥e,即0<a≤
≥e,即0<a≤ 时,f(x)在(0,e]上单调递减,
时,f(x)在(0,e]上单调递减,
f(x)min=f(e)=ae-1=3,a= (舍去).所以,此时f(x)的最小值不是3.
(舍去).所以,此时f(x)的最小值不是3.
综上,存在实数a=e2,使得当x∈(0,e]时,f(x)有最小值3.


科目:高中数学 来源: 题型:
若f(x)是奇函数,且x0是y=f(x)+ex的一个零点,则-x0一定是下列哪个函数的零点( )
A.y=f(-x)ex-1 B.y=f(x)e-x+1
C.y=exf(x)-1 D.y=exf(x)+1
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=x2-1与函数g(x)=alnx(a≠0).
(1)若f(x),g(x)的图象在点(1,0)处有公共的切线,求实数a的值;
(2)设F(x)=f(x)-2g(x),求函数F(x)的极值.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知定义在R上的偶函数f(x),f(1)=0,当x>0时有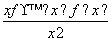 >0,则不等式xf(x)>0的解集为( )
>0,则不等式xf(x)>0的解集为( )
A.{x|-1<x<0} B.{x|x>1或-1<x<0}
C.{x|x>0} D.{x|-1<x<1}
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com