
| A. | 2 | B. | $\sqrt{2}$ | C. | $\frac{{4\sqrt{5}}}{5}$ | D. | $\sqrt{5}$ |
分析 可由这两圆的极坐标方程,在方程的两边同乘以ρ即可得出其平面直角坐标系下的方程,两圆的方程相减,可得公共弦的方程,根据勾股定理即可求出|AB|的值.
解答 解:由ρ=4cosθ得,ρ2=4ρcosθ;
∴x2+y2=4x;
∴(x-2)2+y2=4;
∴该圆表示以(2,0)为圆心,2为半径的圆;
由ρ=2sinθ得,ρ2=2ρsinθ;
∴x2+y2=2y;
∴x2+(y-1)2=1;
∴该圆表示以(0,1)为圆心,1为半径的圆;
两圆的方程相减,可得公共弦的方程为2x-y=0,
(2,0)到直线的距离d=$\frac{4}{\sqrt{5}}$,∴|AB|=2$\sqrt{4-\frac{16}{5}}$=$\frac{4\sqrt{5}}{5}$.
故选C.
点评 考查圆的极坐标方程的表示,以及极坐标和直角坐标互化的公式,以及圆的标准方程,属于中档题.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案科目:高中数学 来源: 题型:解答题
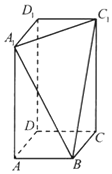 长方体ABCD-A1B1C1D1中,AB=BC=2,过A1,C1,B三点的平面截去长方体的一个角后,得到如图所示的几何体ABCD-A1C1D1,这个几何体的体积为$\frac{40}{3}$
长方体ABCD-A1B1C1D1中,AB=BC=2,过A1,C1,B三点的平面截去长方体的一个角后,得到如图所示的几何体ABCD-A1C1D1,这个几何体的体积为$\frac{40}{3}$查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a>b,c>b,则a>c | B. | 若a>-b,则c-a>c+b | ||
| C. | 若ac2>bc2,则a>b | D. | 若a>b,c>d,则ac>bd |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 各三角形内一点 | B. | 各正三角形的中心 | ||
| C. | 各正三角形的某高线上的点 | D. | 各正三角形外的某点 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com