
分析 (1)求函数的导数,判断函数的单调性,利用函数导数和最值,极值之间的关系进行求解即可.
(2)求函数的导数,判断函数的单调性,利用函数导数和最值,极值之间的关系进行求解即可.
解答 解:(1)f(x)=-x3+3x,x∈[-$\sqrt{3}$,$\sqrt{3}$];
∴f′(x)=-3x2+3=-3(x-1)(x+1),
由f′(x)>0得-1<x<1,此时函数单调递增,
由f′(x)<0得-$\sqrt{3}$<x<-1或1<x<$\sqrt{3}$,此时函数单调递递减,
即当x=-1函数取得极大值f(-1)=1-3=-2,
当x=1函数取得极小值f(1)=-1+3=2,
∵f($\sqrt{3}$)=-3$\sqrt{3}$+3$\sqrt{3}$=0,f(-$\sqrt{3}$)=3$\sqrt{3}$-3$\sqrt{3}$=0,
∴函数的最大值为2,最小值为-2.
(2)f(x)=-x4+2x2+3,x∈[-3,2].
∴f′(x)=-4x3+4x=-4x(x-1)(x+1),
由f′(x)=0得x=0,或x=-1,或x=1,
则当x变化时,f′(x),f(x)的变化如表:
| x | -3 | (-3,-1) | -1 | (-1,0) | 0 | (0,1) | 1 | (1,2) | 2 |
| f′(x) | + | - | + | - | |||||
| f(x) | -60 | 递增 | 极大值4 | 递减 | 极小值3 | 递增 | 极大值4 | 递减 | -5 |
点评 本题主要考查函数在闭区间上的最值,求函数的导数,利用函数最值,极值和导数之间的关系是解决本题的关键.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:高中数学 来源: 题型:解答题
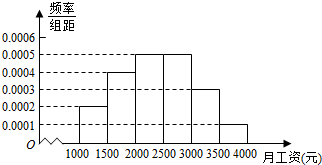 某市统计局就某地居民的月收入调查了10000人,并根据所得数据画出样本的频率分布直方图如图所示.(每个分组包括左端点,不包括右端点,如第一组表示[1000,1500).
某市统计局就某地居民的月收入调查了10000人,并根据所得数据画出样本的频率分布直方图如图所示.(每个分组包括左端点,不包括右端点,如第一组表示[1000,1500).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{4}$=1 | B. | $\frac{{x}^{2}}{12}$+$\frac{{y}^{2}}{8}$=1 | C. | $\frac{{x}^{2}}{12}$+$\frac{{y}^{2}}{4}$=1 | D. | $\frac{{x}^{2}}{4}$+y2=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ESLE后面的语句不可以是条件语句 | |
| B. | 两个条件语句可以共用一个END IF语句 | |
| C. | 条件语句可以没有ELSE后的语句 | |
| D. | 条件语句中IF-THEN语句和ELSE后的语句必须同时存在 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com