
分析 (1)根据抛物线的方程,双曲线的方程,结合它的几何意义,求解抛物线的方程.
(2)联立方程可得,4x2+4(m-1)x+m2=0,由△>0有m<$\frac{3}{2}$,直线y=2x+m,被抛物线所截的弦长的|AB|=$\sqrt{85}$,可求m.
解答 解:(1)∵双曲线为$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{5}$=1,
∴中心为(0,0),a2=4,b2=5
该双曲线的右焦点为(3,0)
∴抛物线方程:y2=12x;
(2)直线y=2x+m,与抛物线y2=12x联立,消去y,可得4x2+4(m-3)x+m2=0
由△>0有16(m-3)2-16m2>0,解得m<$\frac{3}{2}$
设A(x1,y1)B(x2,y2),则x1+x2=3-m,x1x2=$\frac{{m}^{2}}{4}$,
∵直线y=2x+m,被抛物线所截的弦长的|AB|=$\sqrt{85}$,
∴$\sqrt{1+4}$•$\sqrt{(3-m)^{2}-{m}^{2}}$=$\sqrt{85}$,
解得m=-$\frac{4}{3}$,适合m<$\frac{3}{2}$,
∴m=-$\frac{4}{3}$.
点评 本题考查了双曲线,抛物线的几何意义,考查了直线与圆锥曲线的交点问题,运用了韦达定理简化运算,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
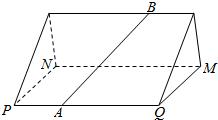 如图,某人沿山坡PQB的直行道AB向上行走,直行道AB与坡脚(直)线PQ成60°角,山坡与地平面所成二面角B-PQ-M的大小为30°.
如图,某人沿山坡PQB的直行道AB向上行走,直行道AB与坡脚(直)线PQ成60°角,山坡与地平面所成二面角B-PQ-M的大小为30°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com