练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    2．10人站成一排，规定在甲、乙两人之间必须有4个人，共有多少种不同的排法？

    分析 由题意知把除甲乙之外的8人中随机抽出4人放在甲乙之间，有C84种可能，甲乙之间的人选出后，甲乙的位置可以互换，故甲乙的位置有2种可能，把甲乙及其中间的4个人看作一个整体与剩下的4个人全排列．

    解答 解：由题意知本题是一个排列组合的实际应用题，
    首先把除甲乙之外的8人中随机抽出4人放在甲乙之间，有C84种可能，他们之间还有一个全排列，
    甲乙之间的人选出后，甲乙的位置可以互换，故甲乙的位置有2种可能，
    最后，把甲乙及其中间的4个人看作一个整体，
    与剩下的4个人全排列是A55=120，
    所以共有A44C84×2×120=493200种．

    点评 本题考查了排列问题的分步计数原理，并且利用捆绑法把甲乙和已选的4人作为一个元素，对于这类题要认真审题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

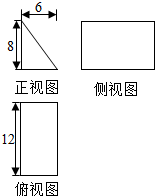    12．一块石材表示的几何体的三视图如图所示，将该石材切削、打磨，加工成球，则能得到的最大球的表面积等于（　　）
    A．$\frac{32π}{3}$B．16πC．32πD．$\frac{16π}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．已知椭圆：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$（a＞b＞0），F1，F2为椭圆的左右焦点，M是椭圆上任一点，若$\overrightarrow{M{F}_{1}}$•$\overrightarrow{M{F}_{2}}$的取值范围是[-4，4]，则椭圆的方程为（　　）
    A．$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{4}$=1B．$\frac{{x}^{2}}{12}$+$\frac{{y}^{2}}{8}$=1C．$\frac{{x}^{2}}{12}$+$\frac{{y}^{2}}{4}$=1D．$\frac{{x}^{2}}{4}$+y2=1

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．对条件语句的描述正确的是（　　）
    A．ESLE后面的语句不可以是条件语句
    B．两个条件语句可以共用一个END IF语句
    C．条件语句可以没有ELSE后的语句
    D．条件语句中IF-THEN语句和ELSE后的语句必须同时存在

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．曲线y=f（x）在点（x0，f（x0）））处的切线的倾斜角是$\frac{π}{4}$，f′（x0）的值为（　　）
    A．$\frac{π}{4}$B．-$\frac{π}{4}$C．-1D．1

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．已知双曲线方程为$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{5}$=1，其右焦点为F．
    （1）求以F为焦点，以双曲线中心为顶点的抛物线方程；
    （2）若直线y=2x+m，被抛物线所截的弦长的|AB|=$\sqrt{85}$，求m的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．已知椭圆的两个焦点分别为F1、F2，其中F1与抛物线x2=8y的焦点重合，过F1且不与x轴平行的直线与椭圆交于A、B两点，若△ABF2为等腰直角三角形，则e2=（　　）
    A．7-4$\sqrt{3}$B．5-2$\sqrt{6}$C．9-6$\sqrt{2}$D．8-2$\sqrt{15}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．△ABC中，角A，B，C的对边分别为a，b，c，a：b：c=2：3：4，则$\frac{sinA-2sinB}{sin2C}$等于（　　）
    A．$\frac{1}{2}$B．2C．-$\frac{1}{2}$D．-2

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．已知函数f（x）=2cos（2x+$\frac{π}{3}$）-2cos2x+1．
    （1）试将函数f（x）化为f（x）=Asin（ωx+φ）+B（ω＞0）的形式，并求该函数的对称中心；
    （2）若锐角△ABC中，A、B、C所对的边分别为a、b、c，且f（A）=0，求$\frac{b}{c}$的取值范围．

    查看答案和解析>>

    同步练习册答案