
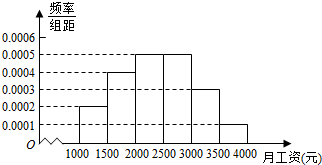
 ij��ͳ�ƾ־�ij�ؾ���������������10000�ˣ��������������ݻ���������Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ����ÿ�����������˵㣬�������Ҷ˵㣬���һ���ʾ[1000��1500����
ij��ͳ�ƾ־�ij�ؾ���������������10000�ˣ��������������ݻ���������Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ����ÿ�����������˵㣬�������Ҷ˵㣬���һ���ʾ[1000��1500�������� ��1������Ƶ��=С���εĸߡ��������
��2��������λ�����������ߵľ��ε��������ȣ�����ֻ���������ʼ����͵���0.5�ĵױߺ������ֵ���ɣ�����ȡ�м�����Ƶ�ʣ�����֮�ͣ�����ɵ�ƽ������
��3�������������[2000��3000�����������÷ֲ�����ij�ȡ���������������ɵô𰸣�
��� �⣺������������[2000��3000����Ƶ��Ϊ��
0.0005����3000-2000��=0.5���� 3��
����0.0002����1500-1000��=0.1��
0.0004����2000-1500��=0.2��
0.0005����2500-2000��=0.25��
0.1+0.2+0.25=0.55��0.5��
���ԣ��������ݵ���λ��Ϊ��
2000+$\frac{0.5-��0.1+0.2��}{0.0005}$=2000+400=2400��Ԫ�� 7��
��������������[2000��3000����Ƶ��Ϊ0.5��10000=5000���ˣ���
�ٴ�10000�����÷ֲ�����������100�ˣ�
����������[2500��3000�������Ӧ��ȡ100��$\frac{5000}{10000}$=50���ˣ�
���� ���⿼����Ƶ�ʷֲ�ֱ��ͼ���ֲ������������ͳ�Ƴ������ͣ���������Ĺؼ�������Ƶ�ʷֲ�ֱ��ͼ��Ƶ����Ƶ�ʣ�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com