
分析 (Ⅰ)由题意可得a=2,由离心率公式可得c,由a,b,c的关系,可得b,进而得到椭圆的方程;
(Ⅱ)设出直线m,n的方程,运用圆和直线相交的弦长公式和直线和椭圆方程联立,运用韦达定理和弦长公式,分别求得|CD|,|AB|,再由四边形的面积公式,化简整理计算即可得到最大值.
解答 解:(Ⅰ)由题意可得2a=4,即a=2,
又e=$\frac{c}{a}$=$\frac{1}{2}$,解得c=1,
b=$\sqrt{{a}^{2}-{c}^{2}}$=$\sqrt{3}$,
则有椭圆C1的方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1;
(Ⅱ)设过点M(1,0)作两条互相垂直的直线m:y=k(x-1),
直线n:y=-$\frac{1}{k}$(x-1),
圆心C2到直线m的距离为d=$\frac{|k|}{\sqrt{1+{k}^{2}}}$,
则|CD|=2$\sqrt{4-{d}^{2}}$=2$\sqrt{\frac{4+3{k}^{2}}{1+{k}^{2}}}$,
由y=-$\frac{1}{k}$(x-1)和椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1,
可得(3k2+4)y2-6ky-9=0,
判别式显然大于0,y1+y2=$\frac{6k}{4+3{k}^{2}}$,y1y2=-$\frac{9}{4+3{k}^{2}}$,
则|AB|=$\sqrt{1+{k}^{2}}$•$\sqrt{({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}}$=$\sqrt{1+{k}^{2}}$•$\sqrt{(\frac{6k}{4+3{k}^{2}})^{2}+\frac{36}{4+3{k}^{2}}}$
=$\frac{12(1+{k}^{2})}{4+3{k}^{2}}$,
则有四边形ABCD面积为S=$\frac{1}{2}$|CD|•|AB|=$\frac{1}{2}$•2$\sqrt{\frac{4+3{k}^{2}}{1+{k}^{2}}}$•$\frac{12(1+{k}^{2})}{4+3{k}^{2}}$
=12•$\sqrt{\frac{1+{k}^{2}}{4+3{k}^{2}}}$=12•$\sqrt{\frac{1}{3+\frac{1}{1+{k}^{2}}}}$,
由于k2>0,即有1+k2>1,S>12×$\frac{1}{2}$=6,且S<12×$\frac{\sqrt{3}}{3}$=4$\sqrt{3}$,
当k不存在,即x=1时,有|CD|=2$\sqrt{4-1}$=2$\sqrt{3}$,|AB|=4,
可得四边形ABCD的面积为$\frac{1}{2}$•2$\sqrt{3}$•4=4$\sqrt{3}$.
则有四边形ABCD的面积的最大值为4$\sqrt{3}$.
点评 本题考查直线和圆、椭圆的位置关系,同时考查直线被圆、椭圆截得弦长的问题,运用圆的垂径定理和弦长公式,以及韦达定理是解题的关键.


 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 25 | B. | 250 | C. | 55 | D. | 133 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
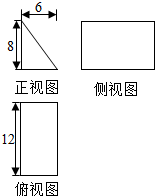 一块石材表示的几何体的三视图如图所示,将该石材切削、打磨,加工成球,则能得到的最大球的表面积等于( )
一块石材表示的几何体的三视图如图所示,将该石材切削、打磨,加工成球,则能得到的最大球的表面积等于( )| A. | $\frac{32π}{3}$ | B. | 16π | C. | 32π | D. | $\frac{16π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
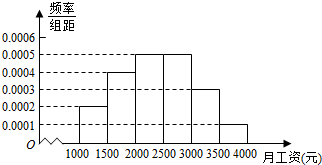 某市统计局就某地居民的月收入调查了10000人,并根据所得数据画出样本的频率分布直方图如图所示.(每个分组包括左端点,不包括右端点,如第一组表示[1000,1500).
某市统计局就某地居民的月收入调查了10000人,并根据所得数据画出样本的频率分布直方图如图所示.(每个分组包括左端点,不包括右端点,如第一组表示[1000,1500).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
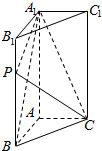 如图,在直三棱柱ABC-A1B1C1中,底面△ABC是直角三角形,AB=AC=1,AA1=2,点P是棱BB1上一点,满足$\overrightarrow{BP}$=λ$\overrightarrow{B{B}_{1}}$(0≤λ≤1).
如图,在直三棱柱ABC-A1B1C1中,底面△ABC是直角三角形,AB=AC=1,AA1=2,点P是棱BB1上一点,满足$\overrightarrow{BP}$=λ$\overrightarrow{B{B}_{1}}$(0≤λ≤1).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{4}$=1 | B. | $\frac{{x}^{2}}{12}$+$\frac{{y}^{2}}{8}$=1 | C. | $\frac{{x}^{2}}{12}$+$\frac{{y}^{2}}{4}$=1 | D. | $\frac{{x}^{2}}{4}$+y2=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ESLE后面的语句不可以是条件语句 | |
| B. | 两个条件语句可以共用一个END IF语句 | |
| C. | 条件语句可以没有ELSE后的语句 | |
| D. | 条件语句中IF-THEN语句和ELSE后的语句必须同时存在 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 2 | C. | -$\frac{1}{2}$ | D. | -2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com