练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    11．对于数25，规定第1次操作为23+53=133，第2次操作为13+33+33=55，如此反复操作，则第2016次操作后得到的数是（　　）
    A．25B．250C．55D．133

    分析 第1次操作为23+53=133，第2次操作为13+33+33=55，第3次操作为53+53=250，第4次操作为23+53+03=133，所以操作结果，以3为周期，循环出现，由此可得第2016次操作后得到的数

    解答 解：第1次操作为23+53=133，
    第2次操作为13+33+33=55，
    第3次操作为53+53=250，
    第4次操作为23+53+03=133
    ∴操作结果，以3为周期，循环出现
    ∵2016=3×672，
    ∴第2016次操作后得到的数与第3次操作后得到的数相同
    ∴第2016次操作后得到的数是250，
    故选：B

    点评 本题考查合情推理，考查学生的阅读能力，解题的关键是得出操作结果，以3为周期，循环出现．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    1．下列命题为真命题的是（　　）
    A．已知x，y∈R，则$\left\{\begin{array}{l}{x＞1}\\{y＞2}\end{array}\right.$是$\left\{\begin{array}{l}{x+y＞3}\\{xy＞2}\end{array}\right.$的充要条件
    B．对空间任意一点O与不共线的三点A，B，C，若$\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{Ob}+z\overrightarrow{OC}$（其中x，y，z∈R），则P，A，B，C四点共面
    C．?a，b∈R，$\frac{a+b}{2}≥\sqrt{ab}$
    D．?x∈R，sinx+cosx=$\frac{7}{5}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

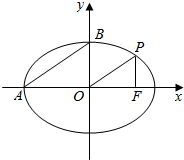    2．如图所示，点P在椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$（a＞b＞0）上，F（c，0）是椭圆的右焦点，点A、B是椭圆的顶点，若PF⊥x轴，且$\frac{|OP|}{|AB|}$=$\frac{c}{a}$，则椭圆的离心率是（　　）
    A．$\frac{1}{2}$B．$\frac{\sqrt{2}}{2}$C．$\frac{1}{3}$D．$\frac{\sqrt{3}}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0），它的一个焦点为F1（-1，0），且经过点M（-1，$\frac{3}{2}$），则椭圆C的方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．已知向量$\overrightarrow{a}$=（1，sinα），$\overrightarrow{b}$=（2，cosα），且$\overrightarrow{a}$∥$\overrightarrow{b}$，计算：$\frac{sinα+2cosα}{cosα-3sinα}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．如图，曲线y=f（x）在点P处的切线方程是y=-x+10，则f（7）+f′（7）=2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．数列{an}的前n项和为Sn，若Sn=2an-1，则an=2n-1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．命题“?x∈R，使得x2+1＞1”的否定为?x∈R，都有x2+1≤1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．椭圆C1：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的长轴长等于圆C2：x2+y2=4的直径，且C1的离心率等于$\frac{1}{2}$，直线l1和l2是过点M（1，0）互相垂直的两条直线，l1交C1于A，B两点，l2交C2于C，D两点．
    （Ⅰ）求C1的标准方程；
    （Ⅱ）求四边形ABCD的面积的最大值．

    查看答案和解析>>

    同步练习册答案