【题目】在平面直角坐标系xOy中，直线l的参数方程为
（t为参数），以原点O为极点，x轴正半轴为极轴建立极坐标系，曲线C的极坐标方程为
，若直线l与曲线C相交于A，B两点，求△AOB的面积．
【答案】12.
【解析】试题分析：（1）先根据极坐标与直角坐标的互化公式得到
的直角坐标方程，利用代入法将直线的参数方程转化为普通方程，利用点到直线距离公式求得三角形的高，将直线的参数方程代入曲线的直角坐标方程，根据韦达定理及直线参数方程的几何意义可求得
，从而根据三角形面积公式可得结果.
试题解析：由曲线C的极坐标方程是
，得ρ2sin2θ=2ρcosθ．
所以曲线C的直角坐标方程是y2=2x．
由直线l的参数方程
(t为参数)，得
，
所以直线l的普通方程为．
将直线l的参数方程代入曲线C的普通方程y2=2x，得
，
设A，B两点对应的参数分别为t1，t2，
所以
，
因为原点到直线的距离
，
所以△AOB的面积是
．
科目：高中数学 来源： 题型：
【题目】已知抛物线
的焦点为
，圆
与
轴的一个交点为
，圆
的圆心为
，
为等边三角形.
（1）求抛物线
的方程
（2）设圆与抛物线交于
、
两点，点
为抛物线上介于、两点之间的一点，设抛物线在点
处的切线与圆交于
、
两点，在圆上是否存在点
，使得直线
、
均为抛物线的切线，若存在求点坐标（用
、
表示）；若不存在，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知某公司为郑州园博园生产某特许商品，该公司年固定成本为10万元，每生产千件需另投入2 .7万元，设该公司年内共生产该特许商品工x千件并全部销售完;每千件的销售收入为R(x)万元，
且
，
(I)写出年利润W(万元〉关于该特许商品x(千件）的函数解析式；
〔II〕年产量为多少千件时，该公司在该特许商品的生产中所获年利润最大?
查看答案和解析>>
科目：高中数学 来源： 题型：
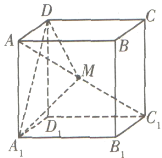
【题目】在棱长为1的正方体
中，点
是对角线
上的动点（点与
不重合），则下列结论正确的是____.
①存在点，使得平面
平面
；
②存在点，使得
平面
；
③
的面积不可能等于
；
④若
分别是
在平面
与平面
的正投影的面积，则存在点，使得
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某专营店经销某商品，当售价不高于10元时，每天能销售100件，当价格高于10元时，每提高1元，销量减少3件，若该专营店每日费用支出为500元，用x表示该商品定价，y表示该专营店一天的净收入（除去每日的费用支出后的收入）．
（1）把y表示成x的函数；
（2）试确定该商品定价为多少元时，一天的净收入最高？并求出净收入的最大值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某中学一位高三班主任对本班50名学生学习积极性和对待班级工作的态度进行调查，得到的统计数据如表所示：
积极参加班级工作 | 不积极参加班级工作 | 合计 | |
学习积极性高 | 18 | 7 | 25 |
学习积极性不高 | 6 | 19 | 25 |
合计 | 24 | 26 | 50 |
（1）如果随机调查这个班的一名学生，那么抽到不积极参加班级工作且学习积极性不高的学生的概率是多少？
（2）若不积极参加班级工作且学习积极性高的7名学生中有两名男生，现从中抽取2名学生参加某项活动，问2名学生中有1名男生的概率是多少？
（3）学生的学习积极性与对待班级工作的态度是否有关系？请说明理由．
附：
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某校高一年级学生全部参加了体育科目的达标测试，现从中随机抽取40名学生的测试成
绩，整理数据并按分数段
，
，
，
，
，
进行分
组，已知测试分数均为整数，现用每组区间的中点值代替该组中的每个数据，则得到体育成绩的折
线图如下：
（1）若体育成绩大于或等于70分的学生为“体育良好”，已知该校高一年级有1000名学生，试估计该校高一年级学生“体育良好”的人数；
（2）为分析学生平时的体育活动情况，现从体育成绩在和的样本学生中随机抽取2人，求所抽取的2名学生中，至少有1人为“体育良好”的概率；
（3）假设甲、乙、丙三人的体育成绩分别为
，
，
，且
，
，
，当三人的体育成绩方差
最小时，写出，，的值（不要求证明）.
注：
，其中
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某校倡导为特困学生募捐，要求在自动购水机处每购买一瓶矿泉水，便自觉向捐款箱中至少投入一元钱．现统计了连续5天的售出矿泉水箱数和收入情况，列表如下：
售出水量 | 7 | 6 | 6 | 5 | 6 |
收入 | 165 | 142 | 148 | 125 | 150 |
学校计划将捐款以奖学金的形式奖励给品学兼优的特困生，规定：特困生综合考核前20名，获一等奖学金500元；综合考核21-50名，获二等奖学金300元；综合考核50名以后的不获得奖学金．
（1）若
与
成线性相关，则某天售出9箱水时，预计收入为多少元？
（2）甲乙两名学生获一等奖学金的概率均为
，获二等奖学金的概率均为
，不获得奖学金的概率均为
，已知甲乙两名学生获得哪个等级的奖学金相互独立，求甲乙两名学生所获得奖学金之和
的分布列及数学期望；
附：回归方程
，其中
．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
