【题目】将正方形ABCD沿对角线BD折成直二面角A-BD-C，下列结论正确的是（ ）
A.AC⊥BDB.△ACD是等边三角形
C.AB与平面BCD成
角D.AB与CD所成的角是60°
【答案】ABD
【解析】
首先画出几何体，由线面垂直的性质定理判断A是否正确；根据直二面角的条件计算
的长度，判断
是否是等边三角形；根据线面角的定义判断C；由异面直线所成的角转化为相交直线所成的角，取
的中点
，连结
，转化为求
或其补角.
A.取
的中点
，连结
,由条件可知
，又
，
所有
平面
，
平面，所有
,所以A正确；
B.设正方形边长为2，则
，且
，所有
，所以是等边三角形，所以B正确；
C.由条件可知
平面
，所以
与平面所成的角为
，所以C不正确；
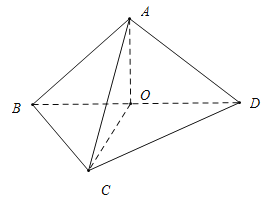
D.取的中点，连结，则
，则
所成的角是或其补角，由以上说明可知
，
,
所以
是等边三角形，所以
，故AB与CD所成的角是60°，所以D正确.
综上可知：ABD正确.
故选：ABD
孟建平名校考卷系列答案科目：高中数学 来源： 题型：
【题目】已知函数
（
为自然对数的底, 
为常数）.
（Ⅰ）讨论函数
的单调性;
（Ⅱ）对于函数
和
,若存在常数
,对于任意
,不等式
都成立,则称直线
是函数
的分界线,设
,问函数
与函数
是否存在“分界线”？若存在,求出常数
;若不存在,说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某校从高一年级参加期末考试的学生中抽出50名学生，并统计了他们的数学成绩（满分为100分），将数学成绩进行分组，并根据各组人数制成如下频率分布表：
（1）写出
的值，并估计本次考试全年级学生的数学平均分（同一组中的数据用该组区间的中点值作代表）；
（2）现从成绩在
内的学生中任选出两名同学，从成绩在
内的学生中任选一名同学，共三名同学参加学习习惯问卷调查活动.若
同学的数学成绩为43分，
同学的数学成绩为
分，求
两同学恰好都被选出的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在三棱柱ABCA1B1C1中，AB AC，点E，F分别在棱BB1，CC1上（均异于端点），且∠ABE∠ACF，AE⊥BB1，AF⊥CC1．
求证：（1）平面AEF⊥平面BB1C1C；
（2）BC //平面AEF．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】阅读如图所示的程序框图，解答下列问题：
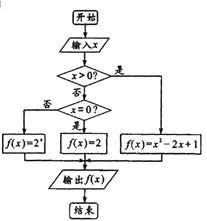
（1）求输入的
的值分别为
时，输出的
的值；
（2）根据程序框图，写出函数
（
）的解析式；并求当关于
的方程
有三个互不相等的实数解时，实数
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在四边形ABCD中，AD∥BC，AD＝AB，∠BCD＝45°，∠BAD＝90°，将△ABD沿BD折起，使平面ABD⊥平面BCD，构成三棱锥A﹣BCD，则在三棱锥A﹣BCD中，下列判断正确的是_____．（写出所有正确的序号）
①平面ABD⊥平面ABC
②直线BC与平面ABD所成角是45°
③平面ACD⊥平面ABC
④二面角C﹣AB﹣D余弦值为
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，四棱锥PABC中，PA⊥底面ABCD，AD∥BC，AB=AD=AC=3，PA=BC=4，M为线段AD上一点，AM=2MD，N为PC的中点.
（Ⅰ）证明MN∥平面PAB;
（Ⅱ）求直线AN与平面PMN所成角的正弦值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆C的方程为
，
为椭圆C的左右焦点，离心率为
，短轴长为2。
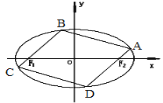
（1）求椭圆C的方程；
（2）如图，椭圆C的内接平行四边形ABCD的一组对边分别过椭圆的焦点，求该平行四边形ABCD面积的最大值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
