
| 统计信息 汽车行驶路线 | 在不堵车的情况下到达城市乙所需时间(天) | 在堵车的情况下到达城市乙所需时间(天) | 堵车的概率 | 运费(万元) |
| 公路1 | 2 | 3 | 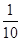 | 1.6 |
| 公路2 | 1 | 4 |  | 0.8 |
 (单位:万元),求
(单位:万元),求 的分布列和数学期望
的分布列和数学期望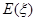 ;
;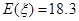 ;(2)选择公路2运送牛奶有可能让牛奶厂获得的毛收入更多.
;(2)选择公路2运送牛奶有可能让牛奶厂获得的毛收入更多. 的值,列出分布列,用期望的计算公式计算出期望;第二问,第二问的情况和第一问一样,先求出走公路2时,毛收入
的值,列出分布列,用期望的计算公式计算出期望;第二问,第二问的情况和第一问一样,先求出走公路2时,毛收入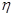 的期望,再比较2个期望
的期望,再比较2个期望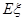 和
和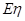 的大小.
的大小.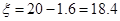 (万元);
(万元);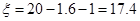 (万元). 2分
(万元). 2分 的分布列为
的分布列为| ξ | 18.4 | 17.4 |
| P | 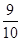 | 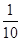 |
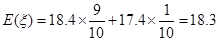 (万元). 5分
(万元). 5分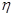 ,则
,则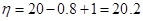 (万元);
(万元);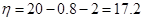 (万元). 7分
(万元). 7分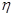 的分布列为
的分布列为| η | 20.2 | 17.2 |
| P |  |  |
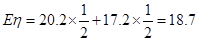 (万元). 10分
(万元). 10分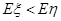 ,
,

科目:高中数学 来源:不详 题型:解答题
 名男生中随机抽取
名男生中随机抽取 名学生测量其身高,据测量被测学生的身高全部在
名学生测量其身高,据测量被测学生的身高全部在 到
到 之间.将测量结果按如下方式分成
之间.将测量结果按如下方式分成 组:第一组
组:第一组 ,第二组
,第二组 , ,第八组
, ,第八组 ,如下右图是按上述分组得到的频率分布直方图的一部分.已知第一组与第八组的人数相同,第六组、第七组和第八组的人数依次成等差数列.
,如下右图是按上述分组得到的频率分布直方图的一部分.已知第一组与第八组的人数相同,第六组、第七组和第八组的人数依次成等差数列.| 分组 | 频数 | 频率 | 频率/组距 |
| | | | |
 |  |  |  |
 |  |  |  |
| | | | |

 名男生,记他们的身高分别为
名男生,记他们的身高分别为 ,求满足:
,求满足: 的事件的概率.
的事件的概率.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
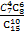 的是( )
的是( )| A.P(X=2) | B.P(X≤2) |
| C.P(X=4) | D.P(X≤4) |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A. | B. | C. | D. |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 粒大小、形状相同但颜色不同的玻璃球的瓶中,随意一次倒出若干粒玻璃球(至少一粒),则倒出奇数粒玻璃球的概率
粒大小、形状相同但颜色不同的玻璃球的瓶中,随意一次倒出若干粒玻璃球(至少一粒),则倒出奇数粒玻璃球的概率 与倒出偶数粒玻璃球的概率
与倒出偶数粒玻璃球的概率 的(大小或相等)关系是 。
的(大小或相等)关系是 。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com