已知对于任意的实数a,b都有(a+b)2≤2(a2+b2)恒成立,则函数f(x)=|sinx|+|cosx|的值域是 .
【答案】
分析:由题意得f(x)>0,利用条件求出f
2(x)的范围,即可得到f(x)的范围.
解答:解:∵对于任意的实数a,b都有(a+b)
2≤2(a
2+b
2)恒成立,函数f(x)=|sinx|+|cosx|>0,
∴f
2(x)=(|sinx|+|cosx|)
2≤2[(|sinx|)
2+(|cosx|)
2]=2,
又∵f
2(x)=(|sinx|+|cosx|)
2=(|sinx|)
2+(|cosx|)
2+2|sinx|•|cosx|≥(|sinx|)
2+(|cosx|)
2=1,
∴1≤f
2(x)≤2,∴1≤f(x)≤
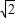
,∴函数f(x)=|sinx|+|cosx|的值域是[1,
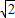
].
故答案为:[1,
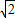
].
点评:本题考查求三角函数的最值的方法,根据f(x)>0,利用条件求出f
2(x)的范围,即可得到f(x)的范围,
体现了转化的数学思想.

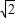 ,∴函数f(x)=|sinx|+|cosx|的值域是[1,
,∴函数f(x)=|sinx|+|cosx|的值域是[1,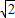 ].
].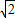 ].
].
