练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图所示是某市2017年4月1日至14日的空气质量指数趋势图，空气质量指数（AQI）小于100表示空气质量优良，空气质量指数大于200表示空气重度污染，某同志随机选择4月1日至4月12日中的某一天到达该市，并停留3天． 该同志到达当日空气质量重度污染的概率 ．

    【答案】
    【解析】解：某同志随机选择4月1日至4月12日中的某一天到达该市，并停留3天． 基本事件总数n=12，
    4月1日至4月12日空气质量重度污染的天数有5天，
    即该同志到达当日空气质量重度污染包含的基本事件个数m=5，
    ∴该同志到达当日空气质量重度污染的概率p= ．
    故答案为： ．
    先求出基本事件总数n=12，再求出该同志到达当日空气质量重度污染包含的基本事件个数m=5，由此能求出该同志到达当日空气质量重度污染的概率．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】椭圆C： =1（a＞b＞0）的离心率为 ，过右焦点F2（c，0）垂直于x轴的直线与椭圆交于A，B两点且|AB|= ，又过左焦点F1（﹣c，0）任作直线l交椭圆于点M
    （1）求椭圆C的方程
    （2）椭圆C上两点A，B关于直线l对称，求△AOB面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知曲线C的参数方程为 （φ为参数），以原点为极点，x轴的非负半轴为极轴建立极坐标系． （Ⅰ）求曲线C的极坐标方程；
    （Ⅱ）已知倾斜角为135°且过点P（1，2）的直线l与曲线C交于M，N两点，求 的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，在三棱柱ABC﹣A1B1C1中，AA1B1B为正方形，BB1C1C为菱形，B1C⊥AC1 ．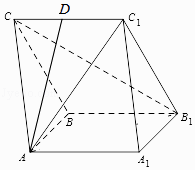
    （Ⅰ）求证：平面AA1B1B⊥平面BB1C1C；
    （Ⅱ）若D是CC1中点，∠ADB是二面角A﹣CC1﹣B的平面角，求直线AC1与平面ABC所成角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】我国南宋数学家秦九韶（约公元1202﹣1261年）给出了求n（n∈N*）次多项式anxn+an﹣1xn﹣1+…+a1x+a0 ， 当x=x0时的值的一种简捷算法．该算法被后人命名为“秦九韶算法”，例如，可将3次多项式改写为a3x3+a2x2+a1x+a0=（（a3x+a2）x+a1）x+a0 ， 然后进行求值．运行如图所示的程序框图，能求得多项式（ ）的值．
    A.x4+x3+2x2+3x+4
    B.x4+2x3+3x2+4x+5
    C.x3+x2+2x+3
    D.x3+2x2+3x+4

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某企业有两个分厂生产某种零件，按规定内径尺寸（单位：mm）的值落在[29.94，30.06）的零件为优质品.从两个分厂生产的零件中各抽出了500件，量其内径尺寸，得结果如下表：

    甲厂：

    分组

    [29.86，29.90）

    [29.90，29.94）

    [29.94，29.98）

    [29.98，30.02）

    [30.02，30.06）

    [30.06，30.10）

    [30.10，30.14）

    频数

    12

    63

    86

    182

    92

    61

    4

    乙厂：

    分组

    [29.86，29.90）

    [29.90，29.94）

    [29.94，29.98）

    [29.98，30.02）

    [30.02，30.06）

    [30.06，30.10）

    [30.10，30.14）

    频数

    29

    71

    85

    159

    76

    62

    18

    （1）试分别估计两个分厂生产的零件的优质品率；

    （2）由以上统计数据填下面列联表，并问是否有的把握认为“两个分厂生产的零件的质量有差异”.

    甲 厂

    乙 厂

    合计

    优质品

    非优质品

    合计

    附：

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】从6双不同手套中，任取4只，

    (1)恰有1双配对的取法是多少？

    (2)没有1双配对的取法是多少？

    (3)至少有1双配对的取法是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某中学准备在开学时举行一次高三年级优秀学生座谈会，拟请20名来自本校高三(1)(2)(3)(4)班的学生参加，各班邀请的学生数如下表所示；

    班级

    高三（1）

    高三（2）

    高三（3）

    高三（4）

    人数

    4

    6

    4

    6

    (1)从这20名学生中随机选出3名学生发言，求这3名学生中任意两个均不属于同一班级的概率；

    (2)从这20名学生中随机选出3 名学生发言，设来自高三（3）的学生数为，求随机变量的概率分布列和数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆 的左右焦点分别为，直线经过椭圆的右焦点与椭圆交于两点，且.

    （I）求直线的方程；

    （II）已知过右焦点的动直线与椭圆交于不同两点，是否存在轴上一定点，使？（为坐标原点）若存在，求出点的坐标；若不存在说明理由.

    查看答案和解析>>

    同步练习册答案