已知函数f(x)=x3+ax2-a2x+2,a∈R.
(1)若a<0时,试求函数y=f(x)的单调递减区间;
(2)若a=0,且曲线y=f(x)在点A、B(A、B不重合)处切线的交点位于直线x=2上,证明:A、B 两点的横坐标之和小于4;
(3)如果对于一切x1、x2、x3∈[0,1],总存在以f(x1)、f(x2)、f(x3)为三边长的三角形,试求正实数a的取值范围.
(1)解:f'(x)=3x
2+2ax-a
2=3(x+a)(x-

)
令f'(x)<0,∵a<0,∴
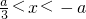
∴函数单调递减区间[

,-a];
(2)证明:当a=0时,f(x)=x
3+2
设在点A(x
1,x
13+2)、B(x
2,x
23+2)处切线的交点位于直线x=2上一点P(2,t),
∵y′=3x
2,∴在点A处的切线斜率为k=
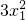
∴在A处的切线方程为y-(x
13+2)=
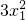
((x-x
1)
∵切线过点P,∴t-(x
13+2)=
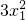
((2-x
1)
∴
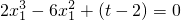
①
同理

②
①-②可得
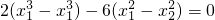
∵x
1≠x
2,∴
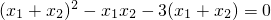
∵x
1≠x
2,∴
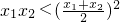
∴
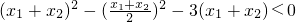
∴0<x
1+x
2<4
∴A、B 两点的横坐标之和小于4;
(3)解:由题设知,f(0)<f(1)+f(1),即2<2(-a
2+a+3),∴-1<a<2
∵a>0,∴0<a<2
∵
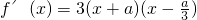
∴x∈

时,f′(x)<0,f(x)单调递减;当x∈
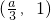
时,f′(x)>0,f(x)单调递增
∴当x=

时,f(x)有最小值f(

)=-
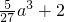
∴f(

)=-
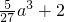
>0①,f(0)<2(-
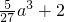
)②,f(1)<2(-
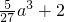
)③,
由①得a<
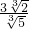
;由②得
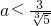
,∵0<a<2,∴
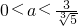
不等式③化为
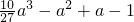
<0
令g(a)=
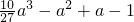
,则g′(a)=
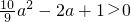
,∴g(a)为增函数
∵g(2)=-

<0,∴当
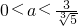
时,g(a)<0恒成立,即③成立
∴正实数a的取值范围为
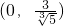
.
分析:(1)求导函数,令f'(x)<0,结合a<0,可得函数单调递减区间;
(2)设在点A(x
1,x
13+2)、B(x
2,x
23+2)处切线的交点位于直线x=2上一点P(2,t),求出切线方程,代入点P的坐标,两方程相减,借助于基本不等式,即可证得A、B 两点的横坐标之和小于4;
(3)先确定0<a<2,再求导函数,确定函数的单调性与最小值,进而可确定正实数a的取值范围.
点评:本题考查导数知识的运用,考查函数的单调性,考查导数的几何意义,考查存在性问题的研究,正确求导是关键.

 )
)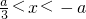
 ,-a];
,-a];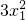
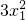 ((x-x1)
((x-x1)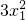 ((2-x1)
((2-x1)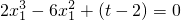 ①
① ②
②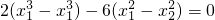
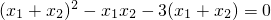
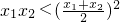
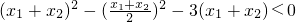
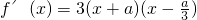
 时,f′(x)<0,f(x)单调递减;当x∈
时,f′(x)<0,f(x)单调递减;当x∈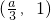 时,f′(x)>0,f(x)单调递增
时,f′(x)>0,f(x)单调递增 时,f(x)有最小值f(
时,f(x)有最小值f( )=-
)=-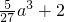
 )=-
)=-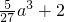 >0①,f(0)<2(-
>0①,f(0)<2(-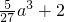 )②,f(1)<2(-
)②,f(1)<2(-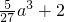 )③,
)③,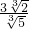 ;由②得
;由②得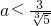 ,∵0<a<2,∴
,∵0<a<2,∴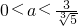
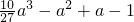 <0
<0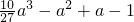 ,则g′(a)=
,则g′(a)=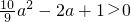 ,∴g(a)为增函数
,∴g(a)为增函数 <0,∴当
<0,∴当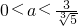 时,g(a)<0恒成立,即③成立
时,g(a)<0恒成立,即③成立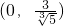 .
.

 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<