
分析 (1)先令y=0,求出方程的实数根,再证明即可,
(2)由条件f(a)>0,根据单调性的定义即可证明f(x)在(0,+∞)上是增函数.
(3)根据不等式的性质即可证明不等式f(a)f(c)<[f(b)]2;
解答 (1)证明:令y=0,∵对任意的正实数x和任意的实数y都有f(xy)=y•f(x).
则f(1)=0,因此x=1是方程f(x)=0一个实数根.
先证明以下结论:
设0<a,a≠1时,假设x,y>0,则存在m,n,使x=am,y=an,
∵对任意的正实数x和任意的实数y都有f(xy)=y•f(x).
∴f(xy)=f(aman)=f(am+n)=(m+n)f(a),
f(x)+f(y)=f(am)+f(an)=mf(a)+nf(a)=(m+n)f(a).
则f(xy)=f(x)+f(y).
令y=0,则f(x)=0,
若方程f(x)=0还有一个实数根,可得f(x)≡0.
与已知f(x)不恒为0矛盾.
因此:方程f(x)=0有且仅有一个实数根;
(2)设xy=ac,则y=logxac,
∴设x0∈(0,1),则f(${a}^{lo{g}_{a}{x}_{0}}$)=(logax0)f(a)<0,
设x1,x2为区间(0,+∞)内的任意两个值,且x1<x2,则0<$\frac{{x}_{1}}{{x}_{2}}$<1,
由(1)可得:
f(x1)-f(x2)=f($\frac{{x}_{1}}{{x}_{2}}$•x2)-f(x2)=f($\frac{{x}_{1}}{{x}_{2}}$)+f(x2)-f(x2)=f($\frac{{x}_{1}}{{x}_{2}}$)<0
所以f(x1)<f(x2),所以f(x)在(0,+∞)上是增函数.
(3)设xy=ac,则y=logxac,
∴f(ac)=f(xy)=yf(x)=(logxac)f(x)=(logxa+logxc)f(x)=(logxa)f(x)+(logxc)f(x)=f(${x}^{lo{g}_{x}a}$)+f(${x}^{lo{g}_{x}c}$)=f(a)+f(c)
∵b2=ac,
∴f(b2)=f(ac),
即2f(b)=f(a)+f(c),
f(b)=$\frac{1}{2}$[f(a)+f(c)],
∴[f(b)]2-f(a)•f(c)=[$\frac{f(a)+f(c)}{2}$]2-f(a)•f(c)=[$\frac{f(a)-f(c)}{2}$]2,
下面证明当x≠1时,f(x)≠0.
假设存在x≠1,f(x0)=0,则对于任意x≠1,f(x)=f(${{x}_{0}}^{lo{g}_{x0}x}$)=(log${\;}_{{x}_{0}}$x)f(x0)=0
不合题意.所以,当x≠1时,f(x)≠0.
因为a>b>c>1,所以存在m≠1,
f(a)-f(c)=f(${m}^{lo{g}_{m}a}$)-f(${m}^{lo{g}_{m}c}$)=(logma-logmc)f(m)≠0,
所以f(a)≠f(c),所以f(a)f(c)<f2(b).
点评 本题主要考查抽象函数应用以及函数单调性的应用,综合考查学生的运算能力,综合性较强,难度较大.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0<a<$\frac{1}{3}$ | B. | a≥$\frac{1}{3}$ | C. | a>$\frac{1}{3}$ | D. | 0<a<$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
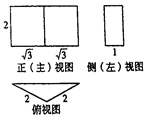
| A. | $\frac{{4\sqrt{3}}}{3}$ | B. | $4\sqrt{3}$ | C. | $2\sqrt{3}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,都有x2<1 | B. | ?x∈R,使得x2≥1 | ||
| C. | ?x∈R,都有x≤-1或x≥1 | D. | ?x∈R,使得x2>1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{8}$ | B. | $\frac{3}{16}$ | C. | $\frac{π}{8}$ | D. | $\frac{π}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com