
���� ��������������������������ʽ�����Ǻ�ȱ任�����f��x���Ľ���ʽ�����������Һ����ĵ����ԣ�����f��x���ĵ����ݼ����䣮
�����������Ҷ������cosC��ֵ���ɵ�C��ֵ�����������Һ����Ķ������ֵ�����f��A������Сֵ���ɵ�m�ķ�Χ��
��� �⣺������$f��x��=\vec a•\vec b=2\sqrt{3}��sinxcosx+�ˣ�sinx+cosx����sinx-cosx��$=$\sqrt{3}$��sin2x-��cos2x
=2�ˣ�$\frac{\sqrt{3}}{2}$sin2x-$\frac{1}{2}$cos2x��=2��sin��2x-$\frac{��}{6}$����
��Ϊf��x�������ֵΪ2�����Խ�æ�=1����$f��x��=2sin��2x-\frac{��}{6}��$��
��$2k��+\frac{��}{2}��2x-\frac{��}{6}��2k��+\frac{3��}{2}$��
�ɵã�$2k��+\frac{2��}{3}��2x��2k��+\frac{5��}{3}$��$k��+\frac{��}{3}��x��k��+\frac{5��}{6}$��
���Ժ���f��x���ĵ���������Ϊ$[{k��+\frac{��}{3}��k��+\frac{5��}{6}}]$��k��Z��
������$cosA=\frac{2b-a}{2c}=\frac{{{b^2}+{c^2}-{a^2}}}{2bc}$���ɵ�2b2-ab=b2+c2-a2��
��b2+a2-c2=ab�����$cosC=\frac{1}{2}$����$C=\frac{��}{3}$��
��Ϊ$0��A��\frac{2��}{3}$����$-\frac{��}{6}��2A-\frac{��}{6}��\frac{7��}{6}$��$-\frac{1}{2}��sin��2A-\frac{��}{6}����1$��
��Ϊ$f��A��-m=2sin��2A-\frac{��}{6}��-m��0$���������$2sin��2A-\frac{��}{6}����m$���������m��-1��
���� ������Ҫ����������������������ʽ�����Ǻ�ȱ任�����Һ����ĵ����ԣ����Ҷ��������Һ����Ķ������ֵ�����ĺ�������⣬�����е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
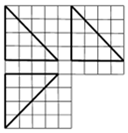
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $-\frac{1}{3}$ | B�� | $\frac{1}{3}$ | C�� | $\frac{{2\sqrt{2}}}{3}$ | D�� | $-\frac{{2\sqrt{2}}}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | 1 | C�� | 2-i | D�� | 3+i |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
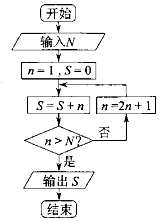
| A�� | 26 | B�� | 57 | C�� | 225 | D�� | 256 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 | [0��10�� | [10��20�� | [20��30�� | [30��40�� | [40��50�� | [50��60] |
| 18����30�� | 6 | 14 | 20 | 32 | 40 | 48 |
| 31����44�� | 4 | 6 | 20 | 28 | 40 | 42 |
| 45����59�� | 22 | 18 | 33 | 37 | 19 | 11 |
| 60�꼰���� | 15 | 13 | 10 | 12 | 5 | 5 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com