
分析 根据条件构造f(x)=nx3+2x-n,求函数的导数,判断函数的导数,求出方程根的取值范围进行求解即可.
解答 解:设f(x)=nx3+2x-n,则f′(x)=3nx2+2,
当n是正整数时,f′(x)>0,则f(x)为增函数,
∵当n≥2时,f($\frac{n}{n+1}$)=n×($\frac{n}{n+1}$)3+2×($\frac{n}{n+1}$)-n=$\frac{n}{(n+1)^{3}}$•(-n2+n+1)<0,
且f(1)=2>0,
∴当n≥2时,方程nx3+2x-n=0有唯一的实数根xn且xn∈($\frac{n}{n+1}$,1),
∴n<(n+1)xn<n+1,an=[(n+1)xn]=n,
因此$\frac{1}{1007}$(a2+a3+a4+…+a2015)=$\frac{1}{1007}$(2+3+4+…+2015)=$\frac{(2+2015)×2014}{2×1007}$=2017,
故答案为:2017.
点评 本题考查递推数列的应用以及函数的单调性的应用函数的零点,数列求和的基本方法,考查分析问题解决问题以及计算能力,综合性较强,难度较大.


科目:高中数学 来源: 题型:选择题
| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
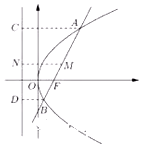 已知抛物线y2=4x的焦点为F,过焦点F的直线l交抛物线于A、B两点,设AB的中点为M,A、B、M在准线上的射影依次为C、D、N.
已知抛物线y2=4x的焦点为F,过焦点F的直线l交抛物线于A、B两点,设AB的中点为M,A、B、M在准线上的射影依次为C、D、N.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 公元263年左右,我国古代数学家刘徽用圆内接正多边形的面积去逼近圆的面积求圆周率π,他从圆内接正六边形算起,令边数一倍一倍地增加,即12,24,48,…,192,…,逐个算出正六边形,正十二边形,正二十四边形,…,正一百九十二边形,…的面积,这些数值逐步地逼近圆面积,刘徽算到了正一百九十二边形,这时候π的近似值是3.141024,刘徽称这个方法为“割圆术”,并且把“割圆术”的特点概括为“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”.刘徽这种想法的可贵之处在于用已知的、可求的来逼近未知的、要求的,用有限来逼近无穷,这种思想及其重要,对后世产生了巨大影响,如图是利用刘徽的“割圆术”思想设计的一个程序框图,若运行改程序(参考数据:$\sqrt{3}$≈1.732,sin15°≈0.2588,sin7.5°≈0.1305),则输出n的值为( )
公元263年左右,我国古代数学家刘徽用圆内接正多边形的面积去逼近圆的面积求圆周率π,他从圆内接正六边形算起,令边数一倍一倍地增加,即12,24,48,…,192,…,逐个算出正六边形,正十二边形,正二十四边形,…,正一百九十二边形,…的面积,这些数值逐步地逼近圆面积,刘徽算到了正一百九十二边形,这时候π的近似值是3.141024,刘徽称这个方法为“割圆术”,并且把“割圆术”的特点概括为“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”.刘徽这种想法的可贵之处在于用已知的、可求的来逼近未知的、要求的,用有限来逼近无穷,这种思想及其重要,对后世产生了巨大影响,如图是利用刘徽的“割圆术”思想设计的一个程序框图,若运行改程序(参考数据:$\sqrt{3}$≈1.732,sin15°≈0.2588,sin7.5°≈0.1305),则输出n的值为( )| A. | 48 | B. | 36 | C. | 30 | D. | 24 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 60° | C. | 30°或150° | D. | 60°或120° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com