
在△ABC中,角A,B,C的对边分别为 ,且A,B,C成等差数列。
,且A,B,C成等差数列。
(1)若 ,
, ,求△ABC的面积;
,求△ABC的面积;
(2)若 成等比数列,试判断△ABC的形状。
成等比数列,试判断△ABC的形状。
(1)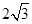 (2)△ABC为等边三角形。
(2)△ABC为等边三角形。
解析试题分析:(1)先由A,B,C成等差数列,解得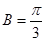 ,然后根据正弦定理得到
,然后根据正弦定理得到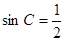 ,再利用面积公式即可;(2)由
,再利用面积公式即可;(2)由 ,
, ,
,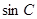 成等比数列,根据正弦定理得
成等比数列,根据正弦定理得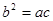 。
。
由余弦定理得
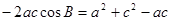 m联立得
m联立得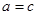 .
.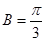 ,故可判断△ABC的形状.
,故可判断△ABC的形状.
试题解析:因为A,B,C成等差数列,所以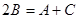 。
。
又A+B+C= ,所以
,所以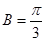 。
。
(1)解法一:因为 ,
, ,所以
,所以
由正弦定理得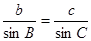 ,即
,即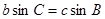 ,即
,即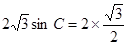 ,得
,得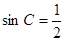 。 因为
。 因为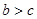 ,所以
,所以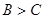 ,即C为锐角,所以
,即C为锐角,所以 ,从而
,从而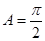 。
。
所以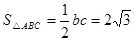 。
。
解法二:由余弦定理得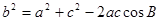 ,
,
即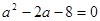 ,得
,得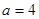 。
。
所以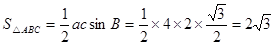 。
。
(2)因为 ,
, ,
,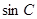 成等比数列,所以
成等比数列,所以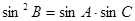 。
。
由正弦定理得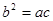 。由余弦定理得
。由余弦定理得
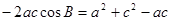 。
。
所以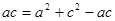 ,即
,即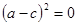 ,即
,即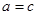 。:Zxxk.Com]
。:Zxxk.Com]
又因为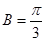 ,所以△ABC为等边三角形。
,所以△ABC为等边三角形。
考点:等差数列、等比数列的基本性质; 正弦定理; 余弦定理; 三角形面积公式.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
如图,半圆O的直径为2,A为直径延长线上的一点,OA=2,B为半圆上任意一点,以AB为一边作等边三角形ABC.问:点B在什么位置时,四边形OACB面积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,公园有一块边长为2的等边△ABC的边角地,现修成草坪, 图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上.
(1)设 (x≥0),
(x≥0), ,求用
,求用 表示
表示 的函数关系式,并求函数的定义域;
的函数关系式,并求函数的定义域;
(2).如果 是灌溉水管,为节约成本,希望它最短,
是灌溉水管,为节约成本,希望它最短, 的位置应在哪里?如果
的位置应在哪里?如果 是参观线路,则希望它最长,
是参观线路,则希望它最长, 的位置又应在哪里?请予证明.
的位置又应在哪里?请予证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com