练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    5．如果关于x的不等式2kx2+kx-$\frac{3}{8}$＜0对一切实数x都成立，那么k的取值范围是（-3，0]．

    分析 根据不等式2kx2+kx-$\frac{3}{8}$＜0对一切实数x都成立，讨论k=0和k≠0时，即可求出k的取值范围．

    解答 解：不等式2kx2+kx-$\frac{3}{8}$＜0对一切实数x都成立，
    k=0时，不等式化为$-\frac{3}{8}$＜0恒成立，
    k≠0时，应满足$\left\{\begin{array}{l}{k＜0}\\{{k}^{2}-8k（-\frac{3}{8}）＜0}\end{array}\right.$，
    解得-3＜k＜0．
    综上，不等式2kx2+kx-$\frac{3}{8}$＜0对一切实数x都成立的k的取值范围是（-3，0]．
    故答案为：（-3，0]．

    点评 本题考查了分类讨论思想的应用问题，也考查了不等式恒成立的问题，是中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    15．下列叙述正确的是（　　）
    A．数列1，3，5，7与7，5，3，1是同一数列
    B．数列0，1，2，3，…的通项公式是an=n
    C．-1，1，-1，1，…是常数列
    D．1，2，22，23，…是递增数列，也是无穷数列

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．（1）已知复数z=3+ai（a∈R）且|z|＜4，求实数a的取值范围．
    （2）记复数z的共轭复数记作$\overline z$，已知$（{1+2i}）\overline z=4+3i$，求z．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．阅读如图所示的程序框图，若输入$a=\frac{10}{21}$，则输出的k值是（　　）
    A．9B．10C．11D．12

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．已知函数$f（x）=cos（\frac{2π}{3}x）+（a-1）sin（\frac{π}{3}x）+a，g（x）={2^x}-{x^2}$，若f[g（x）]≤0对x∈[0，1]恒成立，则实数a的取值范围是（　　）
    A．$（-∞，\sqrt{3}-1]$B．（-∞，0]C．[0，$\sqrt{3}$-1]D．$（-∞，1-\sqrt{3}]$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．设函数f（x）=-x2+4x-3，若从区间[2，6]上任取一个数x0，则所选取的实数x0满足f（x0）≥0的概率为（　　）
    A．$\frac{1}{4}$B．$\frac{1}{3}$C．$\frac{1}{2}$D．$\frac{3}{4}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．已知函数 f（x）=kx（$\frac{1}{e}$≤x≤e2），与函数$g（x）={（\frac{1}{e}）^{\frac{x}{2}}}$，若f（x）与g（x）的图象上分别存在点M，N，使得MN关于直线y=x对称，则实数k的取值范围是（　　）
    A．[-$\frac{1}{e}$，e]B．[-$\frac{2}{e}$，2e]C．（-$\frac{2}{e}$，2e）D．[-$\frac{3}{e}$，3e]

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．已知函数f（x）=x2-6x-9，则函数f（x）在x∈（1，4）的值域是[-18，-14）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

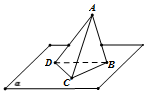    15．如图，三棱锥A-BCD的顶点B、C、D在平面α内，CA=AB=BC=CD=DB=4，AD=2$\sqrt{6}$，若将该三棱锥以BC为轴转动，到点A落到平面α内为止，则A、D两点所经过的路程之和是  $2\sqrt{3}π$．

    查看答案和解析>>

    同步练习册答案