
���� ��1���ȸ����������µ����ˮ��ΪxԪ/kw•h��������֪�õ�������$\frac{k}{x-0.4}$+a�����ɼ������棻
��2�������⣺��ˮ����Ͷ�Ϊ����ʱ�Կɱ�֤��ˮ�ֵ������������������20%���õ�����x�IJ��ȹ�ϵ����˲���ʽ���ɵý⣮
��� �⣺��1�������µ����ˮ��ΪxԪ/kw•h��������֪��ˮ������$\frac{k}{x-0.4}$+a����ˮ�ֵ�����Ϊ��
y=��$\frac{k}{x-0.4}$+a����x-0.3������0.55��x��0.75����
��2����������$\left\{\begin{array}{l}{��\frac{0.2a}{x-0.4}+a����x-0.3����[a����0.8-0.3��]��1+20%��}\\{0.55��x��0.75}\end{array}\right.$��
������$\left\{\begin{array}{l}{{x}^{2}-1.1x+0.3��0}\\{0.55��x��0.75}\end{array}\right.$��
��˲���ʽ��0.60��x��0.75��
�𣺵�ˮ����Ͷ�Ϊ0.6xԪ/kw•h�Կɱ�֤��ˮ�ֵ������������������20%��
���� ��С����Ҫ���齨��������ϵ���ⲻ��ʽ�Ȼ���֪ʶ�������ۺ�Ӧ����ѧ֪ʶ��˼��ͷ������ʵ������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
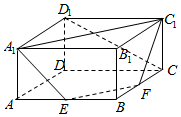 ��ͼ���ڳ�����ABCD-A1B1C1D1�У�AA1=1��AB=AD=2��E��F�ֱ�����AB��BC���е㣮֤��A1��C1��F��E�ĵ㹲�棬����ֱ��CD1��ƽ��A1C1FE���ɽǵ�����ֵ��
��ͼ���ڳ�����ABCD-A1B1C1D1�У�AA1=1��AB=AD=2��E��F�ֱ�����AB��BC���е㣮֤��A1��C1��F��E�ĵ㹲�棬����ֱ��CD1��ƽ��A1C1FE���ɽǵ�����ֵ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
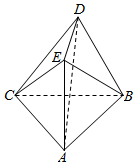 ��ͼ���ռ伸����ABCDE�У�ƽ��ABC��ƽ��BCD��AE��ƽ��ABC��
��ͼ���ռ伸����ABCDE�У�ƽ��ABC��ƽ��BCD��AE��ƽ��ABC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
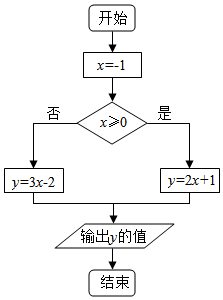
| A�� | -5 | B�� | 5 | C�� | -1 | D�� | -2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com