
如图,直线l1和l2相交于点M,l1⊥l2,点N∈l1.以A、B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等.若△AMN为锐角三角形,|AM|= ,|AN|=3,且|BN|=6.建立适当的坐标系,求曲线段C的方程.(14分)
,|AN|=3,且|BN|=6.建立适当的坐标系,求曲线段C的方程.(14分)

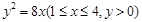
【解析】
试题分析:如图建立坐标系,以l1为x轴,MN的垂直平分线为y轴,点O为坐标原点.由题意可知:曲线C是以点N为焦点,以l2为准线的抛物线的一段,其中A、B分别为C的端点.
设曲线段C的方程为 ,其中
,其中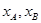 分别为A、B的横坐标,
分别为A、B的横坐标,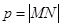 .所以,
.所以,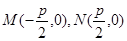 .
由
.
由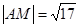 ,
,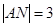 得
得
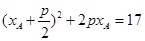 ①
①
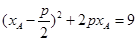 ②
②
联立①②解得 .将其代入①式并由p>0解得
.将其代入①式并由p>0解得 ,或
,或 .
.
因为△AMN为锐角三角形,所以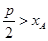 ,故舍去
,故舍去 . ∴p=4,
. ∴p=4,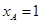 .
.
由点B在曲线段C上,得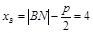 .综上得曲线段C的方程为
.综上得曲线段C的方程为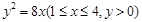 .
.
考点:本题主要考查抛物线的标准方程、几何性质及直线与抛物线的位置关系,
点评:这是一道综合性较强的题目,在重点考查抛物线标准方程、几何性质同时,考查了直线与直线的位置关系,对考生分析问题解决问题的能力及运算能力都有较好的考查功能。


科目:高中数学 来源: 题型:
 如图,直线l1和l2相交于点M,l1⊥l2,点N∈l1.以A,B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等.若△AMN为锐角三角形,|AM|=
如图,直线l1和l2相交于点M,l1⊥l2,点N∈l1.以A,B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等.若△AMN为锐角三角形,|AM|=| 17 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,直线l1和l2相交于点M且l1⊥l2,点N∈l1.以A、B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等.若△AMN为锐角三角形,|AM|=
如图,直线l1和l2相交于点M且l1⊥l2,点N∈l1.以A、B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等.若△AMN为锐角三角形,|AM|=| 17 |
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,直线l1和l2相交于点M,l1⊥l2,点N∈l1.以A、B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等.若△AMN为锐角三角形,|AM|=![]() ,|AN|=3,且|BN|=6.建立适当的坐标系,求曲线段C的方程
,|AN|=3,且|BN|=6.建立适当的坐标系,求曲线段C的方程

查看答案和解析>>
科目:高中数学 来源:2012年人教A版高中数学选修1-1 2.3抛物线练习卷(解析版) 题型:解答题
如图,直线l1和l2相交于点M,l1⊥l2,点N∈l1.以A、B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等.若△AMN为锐角三角形,|AM|= ,|AN|=3,且|BN|=6.建立适当的坐标系,求曲线段C的方程.(14分)
,|AN|=3,且|BN|=6.建立适当的坐标系,求曲线段C的方程.(14分)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com