练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    10．某课题组对全班45名同学的饮食习惯进行了一次调查，并用茎叶图表示45名同学的饮食指数，说明：图中饮食指数低于70的人被认为喜食蔬菜，饮食指数不低于70的人被认为喜食肉类．
    （1）求饮食指数在[10，39]女同学中选取2人，恰有1人在[20，29]中的概率．
    （2）根据茎叶图，完成2×2列联表，并判断是否有90%的把握认为喜食蔬菜还是喜食肉类与性别有关，说明理由．
    喜食蔬菜喜食肉类合计
    男同学
    女同学
    合计
    参考公式：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$
    如表临界值表仅供参考：
    P（k2≥k）0.1000.0500.010
    k2.7063.8416.635

    分析 （1）根据茎叶图中的数据，求出饮食指数在[10，39]内的女同学数，利用列表法求出基本事件数，计算对应的概率即可；
    （2）根据茎叶图，填写2×2列联表，利用公式计算观测值K2，对照数表即可得出结论．

    解答 解：（1）根据茎叶图中的数据，知；
    饮食指数在[10，39]内的女同学有5人，
    分别是[10，19]内1人，记为A，
    [20，29]内1人，记为B，
    [30，39]内3人，记为C，D，E；
    从这5人中选取2人，基本事件为AB，AC，AD，AE，BC，BD，BE，CD，CE，DE共10种；
    恰有1人在[20，29]中事件是AB，BC，BD，BE共4种；
    所求的概率为P=$\frac{4}{10}$=0.4；
    （2）根据茎叶图，填写2×2列联表，如下；

    喜食蔬菜喜食肉类合计
    男同学19625
    女同学17320
    合计36945
    计算观测值K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$=$\frac{45{×（19×3-17×6）}^{2}}{36×9×20×25}$=0.5625＜2.706；
    对照数表得出，没有90%的把握认为喜食蔬菜还是喜食肉类与性别有关．

    点评 本题考查了用列举法求古典概型的概率问题，也考查了独立性检验的应用问题，是基础题目．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    1．已知各项均为正数的数列{an}满足a1=1，an+2=1+$\frac{1}{{a}_{n}}$（n∈N*），若a2014=a2016，则a13+a2016=$\frac{21}{13}$+$\frac{1+\sqrt{5}}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．求圆O1：x2+y2+4x-4y+7=0关于直线x-2y-1=0对称的圆的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．求过点A（4，1）且符合下列条件的直线方程．
    （1）在y轴上的截距是在x轴上截距的3倍；
    （2）在两坐标轴上的截距和为10．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．在平面直角坐标系xOy中，曲线C1，C2的参数方程分别为$\left\{\begin{array}{l}{x=t}\\{y={t}^{2}}\end{array}\right.$（t为参数）和$\left\{\begin{array}{l}{x=\sqrt{2}cosα}\\{y=\sqrt{2}sinα}\end{array}\right.$（α为参数）．
    （1）将曲线C1，C2的参数方程化为普通方程，并指出是何种曲线；
    （2）以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系，求曲线C1，C2的交点所确定的直线的极坐标方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

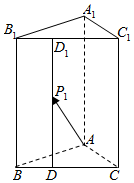    15．如图，在三棱柱ABC-A1B1C1中，AA1⊥底面ABC，AB=AC=$\sqrt{3}$，BC=3，AA1=5，$\overrightarrow{BD}$=$\frac{1}{3}\overrightarrow{BC}$，$\overrightarrow{{B}_{1}{D}_{1}}$=$\frac{1}{3}\overrightarrow{{B}_{1}{C}_{1}}$，$\overrightarrow{D{P}_{1}}$=$\frac{3}{5}\overrightarrow{D{D}_{1}}$，一光线从A射出，第一次射到平面BCC1B1上点P1，经反射后第二次射到表面上点P2，依次下去，…，则P2P3=（　　）
    A．$\frac{\sqrt{10}}{6}$B．$\frac{\sqrt{10}}{4}$C．$\frac{\sqrt{10}}{3}$D．$\frac{\sqrt{10}}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．已知直线l1为曲线y=x2+x-2在点（0，-2）处的切线，l2为该曲线的另一条切线，且l1⊥l2．
    ①求直线l1的方程；
    ②求直线l2的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的实轴为A1A2，虚轴的一个端点为B，若三角形A1A2B的面积为$\sqrt{2}$b2，则双曲线的离心率（　　）
    A．$\frac{\sqrt{6}}{3}$B．$\frac{\sqrt{6}}{2}$C．$\sqrt{2}$D．$\sqrt{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．把复数z的共轭复数记作$\overline{z}$，已知（1+i）$\overline{z}$=1-i，则z=i．

    查看答案和解析>>

    同步练习册答案