
分析 各项均为正数的数列{an}满足a1=1,an+2=1+$\frac{1}{{a}_{n}}$(n∈N*),a2014=a2016,可得a2016=1+$\frac{1}{{a}_{2014}}$,化简解出a2014=$\frac{1+\sqrt{5}}{2}$=a2016.由a1=1,an+2=1+$\frac{1}{{a}_{n}}$(n∈N*),可得a3=2,依此类推可得:a13=$\frac{21}{13}$.即可得出.
解答 解:∵各项均为正数的数列{an}满足a1=1,an+2=1+$\frac{1}{{a}_{n}}$(n∈N*),a2014=a2016,
∴a2016=1+$\frac{1}{{a}_{2014}}$,即a2014=1+$\frac{1}{{a}_{2014}}$,化为${a}_{2014}^{2}$-a2014-1=0,解得a2014=$\frac{1+\sqrt{5}}{2}$=a2016.
∵a1=1,an+2=1+$\frac{1}{{a}_{n}}$(n∈N*),∴a3=2,a5=$\frac{3}{2}$,a7=$\frac{5}{3}$,a9=$\frac{8}{5}$,a11=$\frac{13}{8}$,a13=$\frac{21}{13}$.
则a13+a2016=$\frac{21}{13}$+$\frac{1+\sqrt{5}}{2}$.
故答案为:$\frac{21}{13}$+$\frac{1+\sqrt{5}}{2}$.
点评 本题考查了递推关系、方程的解法,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
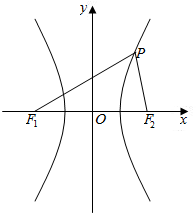 已知双曲线的中心在坐标原点,焦点在x轴上,F1,F2分别为左、右焦点,双曲线的右支上有一点P,∠F1PF2=$\frac{π}{3}$,且△PF1F2的面积为2$\sqrt{3}$,又双曲线的离心率为2,求该双曲线的方程.
已知双曲线的中心在坐标原点,焦点在x轴上,F1,F2分别为左、右焦点,双曲线的右支上有一点P,∠F1PF2=$\frac{π}{3}$,且△PF1F2的面积为2$\sqrt{3}$,又双曲线的离心率为2,求该双曲线的方程.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 收缩压范围 | 89.5~104.4 | 104.5~119.4 | 119.5~134.4 | 134.5~149.4 | 149.5~164.4 | 164.5~179.4 |
| 人数 | 24 | 62 | 72 | 26 | 12 | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
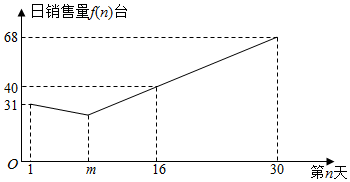
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某课题组对全班45名同学的饮食习惯进行了一次调查,并用茎叶图表示45名同学的饮食指数,说明:图中饮食指数低于70的人被认为喜食蔬菜,饮食指数不低于70的人被认为喜食肉类.
某课题组对全班45名同学的饮食习惯进行了一次调查,并用茎叶图表示45名同学的饮食指数,说明:图中饮食指数低于70的人被认为喜食蔬菜,饮食指数不低于70的人被认为喜食肉类.| 喜食蔬菜 | 喜食肉类 | 合计 | |
| 男同学 | |||
| 女同学 | |||
| 合计 |
| P(k2≥k) | 0.100 | 0.050 | 0.010 |
| k | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com