
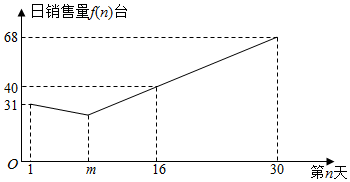
分析 (1)根据题意,当m≤n≤30时,设f(n)=kn+b,(n∈N*),利用f(16)=40,f(30)=68,求出参数,进而得到f (n)的表达式;
(2)利用1≤n≤m时,函数f(n)=32-n;当m≤n≤30时,f(n)=2n+8,建立方程,求出m,利用等差数列的求和公式求出前m天此型号空调的销售总量;
(3)设该店此型号空调销售到第x天时,才可被认为开始旺销,则销售总量220+$\frac{(x-8)(26+2x+8)}{2}$≥570,求出x,即可得出结论.
解答 解:(1)根据题意,当m≤n≤30时,设f(n)=kn+b,(n∈N*)
∵f(16)=40,f(30)=68,
∴$\left\{\begin{array}{l}{16k+b=40}\\{30k+b=68}\end{array}\right.$,∴k=2,b=8,
∴f(n)=2n+8(m≤n≤30),
(2)∵1≤n≤m时,函数f(n)=32-n;当m≤n≤30时,f(n)=2n+8,
∴32-m=2m+8,∴m=8.
∴该店前m天此型号空调的销售总量$\frac{8(31+24)}{2}$=220台;
(3)设该店此型号空调销售到第x天时,才可被认为开始旺销,则销售总量220+$\frac{(x-8)(26+2x+8)}{2}$≥570,
∴x2+9x-386≥0,∴x≥18,
∴设该店此型号空调销售到第18天时,才可被认为开始旺销.
点评 已知函数图象求函数的解析式,是一种常见的题型,关键是要知道函数的类型,利用待定系数法设出函数的解析式,然后将函数图象上的点的坐标代入求出参数的值,即可得到要求函数的解析式.


科目:高中数学 来源: 题型:解答题
| 区间 | 人数 | 频率 | |
| 第1组 | [25,30) | 50 | 0.1 |
| 第2组 | [30,35) | 50 | 0.1 |
| 第3组 | [35,40) | a | 0.4 |
| 第4组 | [40,45) | 150 | b |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{6}}{3}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com