
在 中,
中, 分别是角
分别是角 的对边,
的对边, 为
为 的面积,若
的面积,若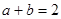 ,且
,且
(1).求 的值; (2).求
的值; (2).求 的最大值。
的最大值。
科目:高中数学 来源: 题型:解答题
如图,海船甲位于岛屿A的南偏西60°方向的B处,且与岛屿A相距2海里,渔船乙以10海里/小时的速度从岛屿A出发沿正北方向航行,若渔船甲同时从B处出发沿北偏东 的方向追赶渔船乙,刚好用2小时追上。
的方向追赶渔船乙,刚好用2小时追上。
①求渔船甲的速度;
②求 的值。
的值。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,某小区准备在一直角围墙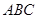 内的空地上植造“绿地
内的空地上植造“绿地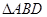 ”,其中
”,其中 ,
,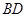 长可根据需要进行调节(
长可根据需要进行调节(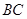 足够长),现规划在
足够长),现规划在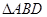 内接正方形
内接正方形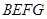 内种花,其余地方种草,设种草的面积
内种花,其余地方种草,设种草的面积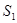 与种花的面积
与种花的面积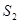 的比
的比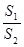 为
为 ,
,
(1)设角 ,将
,将 表示成
表示成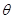 的函数关系;
的函数关系;
(2)当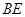 为多长时,
为多长时, 有最小值,最小值是多少?
有最小值,最小值是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com