
已知AB是圆O的直径,C为圆O上一点,CD⊥AB于点D,弦BE与CD、AC分别交于点M、N,且MN=MC
(1)求证:MN=MB;
(2)求证:OC⊥MN。
详见解析
解析试题分析:(1)连结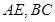 ,根据直径所对的圆周角是直角,得
,根据直径所对的圆周角是直角,得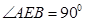 ,根据等量代换得
,根据等量代换得 ,最后利用三角形的性质即可得出
,最后利用三角形的性质即可得出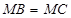 ,从而得到
,从而得到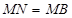 ;
;
(2)设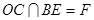 ,根据
,根据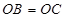 ,得到
,得到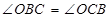 ,再由(1)知,
,再由(1)知, ,等量代换得
,等量代换得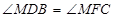 ,即
,即 即可证出结论.此题比较基础,属于基础题型,平时多加练习,能够拿满分.
即可证出结论.此题比较基础,属于基础题型,平时多加练习,能够拿满分.
试题解析:证明:(1)连结AE,BC,∵AB是圆O的直径,∴∠AEB=90°,∠ACB=90°∵MN=MC,∴∠MCN=∠MNC又∵∠ENA=∠MNC,∴∠ENA=∠MCN∴∠EAC=∠DCB,∵∠EAC=∠EBC,∴∠MBC=∠MCB,∴MB=MC∴MN=MB. 5分
(2)设OC∩BE=F,∵OB=OC,∴∠OBC=∠OCB
由(1)知,∠MBC=∠MCB,∴∠DBM=∠FCM.又∵∠DMB=∠FMC
∴∠MDB=∠MFC,即∠MFC=90°∴OC⊥MN. 10分
考点:与圆有关的问题


科目:高中数学 来源: 题型:解答题
已知 和
和 相交于A、B两点,过A点作
相交于A、B两点,过A点作 切线交
切线交 于点E,连接EB并延长交
于点E,连接EB并延长交 于点C,直线CA交
于点C,直线CA交 于点D,
于点D,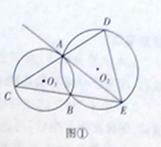

(1)当点D与点A不重合时(如图1),证明:ED2=EB·EC;
(2)当点D与点A重合时(如图2),若BC=2,BE=6,求 的直径长.
的直径长.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图, 是圆
是圆 的直径,
的直径, 是
是 延长线上的一点,
延长线上的一点, 是圆
是圆 的割线,过点
的割线,过点 作
作 的垂线,交直线
的垂线,交直线 于点
于点 ,交直线
,交直线  于点
于点 ,过点
,过点 作圆
作圆 的切线,切点为
的切线,切点为 .
.
(1)求证: 四点共圆;(2)若
四点共圆;(2)若 ,求
,求 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图所示,D,E分别为△ABC的边AB,AC上的点,且不与△ABC的顶点重合.已知AE的长为m,AC的长为n,AD,AB的长是关于x的方程x2-14x+mn=0的两个根.
(1)证明:C,B,D,E四点共圆;
(2)若∠A=90°,且m=4,n=6,求C,B,D,E所在圆的半径.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,D,E分别为△ABC边AB,AC的中点,直线DE交△ABC的外接圆于F,G两点,若CF∥AB,证明:
(1)CD=BC;
(2)△BCD∽△GBD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com