
【题目】已知函数f(x)是定义在R上的偶函数,当x≥0时,f(x)=x2﹣2x﹣1.
(1)求f(x)的函数解析式;
(2)作出函数f(x)的简图,写出函数f(x)的单调减区间及最值.
(3)若关于x的方程f(x)=m有两个解,试说出实数m的取值范围.(只要写出结果,不用给出证明过程)
【答案】
(1)解:当x<0时,﹣x>0,f(﹣x)=x2+2x﹣1.
∵f(x)是定义在R上的偶函数,∴f(﹣x)=f(x)
∴f(x)=x2+2x﹣1
∴f(x)= ![]()
(2)解:函数图象如图所示
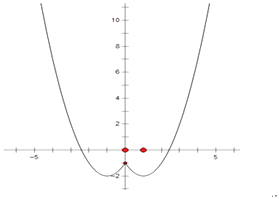
单调减区间为(﹣∞,﹣1],[0,1]
f(x)min=﹣2,函数没有最大值
(3)解:m∈{﹣2}∪(﹣1,+∞)
【解析】(1)当x<0时,﹣x>0,由已知中当x≥0时,f(x)=x2﹣2x﹣1,及函数f(x)是定义在R上的偶函数,可求出当x<0时函数的解析式,进而得到答案,(2)由二次函数的图象画法可得到函数的草图;根据图象下降对应函数的单调递减区间,分析出函数值的取值范围后可得到答案;(3)由图象可得结论.
【考点精析】本题主要考查了函数奇偶性的性质的相关知识点,需要掌握在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇才能正确解答此题.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:
【题目】如下图,三棱柱ABC-A1B1Cl中,M,N分别为CC1,A1B1的中点.CA⊥CB1,CA=CB1,BA=BC=BB1.
(I)求证:直线MN//平面CAB1;
(II)求证:直线BA1⊥平面CAB1.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,等腰梯形![]() 的底角
的底角 ![]() 等于
等于![]() ,直角梯形
,直角梯形 ![]() 所在的平面垂直于平面
所在的平面垂直于平面![]() ,
, ![]() ,且
,且![]() .
.
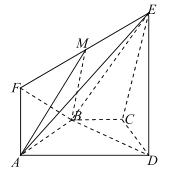
(1)证明:平面![]() 平面
平面![]() ;
;
(2)点![]() 在线段
在线段![]() 上,试确定点
上,试确定点![]() 的位置,使平面
的位置,使平面![]() 与平面
与平面![]() 所成二面角的余弦值为
所成二面角的余弦值为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ﹣
﹣ ![]() 的定义域为集合A,B={x∈Z|3<x<11},C={x∈R|x<a或x>a+1}.
的定义域为集合A,B={x∈Z|3<x<11},C={x∈R|x<a或x>a+1}.
(1)求A,(RA)∩B;
(2)若A∪C=R,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某创业投资公司拟投资开发某种新能源产品,估计能获得10万元到1 000万元的投资收益.现准备制定一个对科研课题组的奖励方案:奖金y(单位:万元)随投资收益x(单位:万元)的增加而增加,且奖金不超过9万元,同时奖金不超过投资收益的20%.
(1)请分析函数y= ![]() +1是否符合公司要求的奖励函数模型,并说明原因;
+1是否符合公司要求的奖励函数模型,并说明原因;
(2)若该公司采用函数模型y= ![]() 作为奖励函数模型,试确定最小的正整数a的值.
作为奖励函数模型,试确定最小的正整数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】股票市场的前身是起源于1602年荷兰人在阿姆斯特河大桥上进行荷属东印度公司股票的买卖,而正规的股票市场最早出现在美国.2017年2月26号,中国证监会主席刘士余谈了对股市的几点建议,给广大股民树立了信心.最近,张师傅和李师傅要将家中闲置资金进行投资理财.现有两种投资方案,且一年后投资盈亏的情况如下:
(1)投资股市:
投资结果 | 获利 | 不赔不赚 | 亏损 |
概率 |
|
|
|
(2)购买基金:
投资结果 | 获利 | 不赔不赚 | 亏损 |
概率 |
|
|
|
(Ⅰ)当![]() 时,求
时,求![]() 的值;
的值;
(Ⅱ)已知“购买基金”亏损的概率比“投资股市”亏损的概率小,求![]() 的取值范围;
的取值范围;
(Ⅲ)已知张师傅和李师傅两人都选择了“购买基金”来进行投资,假设三种投资结果出现的可能性相同,求一年后他们两人中至少有一人获利的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 与直线
与直线![]() 相切.
相切.
(1)若直线![]() 与圆
与圆![]() 交于
交于![]() 两点,求
两点,求![]() ;
;
(2)设圆![]() 与
与![]() 轴的负半轴的交点为
轴的负半轴的交点为![]() ,过点
,过点![]() 作两条斜率分别为
作两条斜率分别为![]() 的直线交圆
的直线交圆![]() 于
于![]() 两点,且
两点,且![]() ,试证明直线
,试证明直线![]() 恒过一定点,并求出该定点的坐标.
恒过一定点,并求出该定点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com