
【题目】已知圆![]() 与直线
与直线![]() 相切.
相切.
(1)若直线![]() 与圆
与圆![]() 交于
交于![]() 两点,求
两点,求![]() ;
;
(2)设圆![]() 与
与![]() 轴的负半轴的交点为
轴的负半轴的交点为![]() ,过点
,过点![]() 作两条斜率分别为
作两条斜率分别为![]() 的直线交圆
的直线交圆![]() 于
于![]() 两点,且
两点,且![]() ,试证明直线
,试证明直线![]() 恒过一定点,并求出该定点的坐标.
恒过一定点,并求出该定点的坐标.
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的偶函数,当x≥0时,f(x)=x2﹣2x﹣1.
(1)求f(x)的函数解析式;
(2)作出函数f(x)的简图,写出函数f(x)的单调减区间及最值.
(3)若关于x的方程f(x)=m有两个解,试说出实数m的取值范围.(只要写出结果,不用给出证明过程)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F1,F2分别为双曲线![]() 的左、右焦点,P为双曲线右支上的任意一点,若
的左、右焦点,P为双曲线右支上的任意一点,若![]() 的最小值为8a,则双曲线的离心率e的取值范围是( )
的最小值为8a,则双曲线的离心率e的取值范围是( )
A. (1,+∞) B. (1,2] C. (1,![]() ] D. (1,3]
] D. (1,3]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有三支股票![]() ,
, ![]() ,
, ![]() ,28位股民的持有情况如下:每位股民至少持有其中一支股票,在不持有
,28位股民的持有情况如下:每位股民至少持有其中一支股票,在不持有![]() 股票的人中,持有
股票的人中,持有![]() 股票的人数是持有
股票的人数是持有![]() 股票的人数的2倍.在持有
股票的人数的2倍.在持有![]() 股票的人中,只持有
股票的人中,只持有![]() 股票的人数比除了持有
股票的人数比除了持有![]() 股票外,同时还持有其它股票的人数多1.在只持有一支股票的人中,有一半持有
股票外,同时还持有其它股票的人数多1.在只持有一支股票的人中,有一半持有![]() 股票.则只持有
股票.则只持有![]() 股票的股民人数是( )
股票的股民人数是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的通项为an , 前n项和为sn , 且an是sn与2的等差中项,数列{bn}中,b1=1,点P(bn , bn+1)在直线x﹣y+2=0上. (Ⅰ)求数列{an}、{bn}的通项公式an , bn
(Ⅱ)设{bn}的前n项和为Bn , 试比较 ![]() 与2的大小.
与2的大小.
(Ⅲ)设Tn= ![]() ,若对一切正整数n,Tn<c(c∈Z)恒成立,求c的最小值.
,若对一切正整数n,Tn<c(c∈Z)恒成立,求c的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了引导居民合理用水,居民生活用水实行二级阶梯式水价计量办法,具体如下:第一阶梯,每户居民月用水量不超过12吨,价格为4元/吨;第二阶梯,每户居民月用水量超过12吨,超过部分的价格为8元/吨.为了了解全市居民月用水量的分布情况,通过抽样获得了100户居民的月用水量(单位:吨),将数据按照![]() ,
, ![]() ,…,
,…, ![]() 分成8组,制成了如图1所示的频率分布直方图.
分成8组,制成了如图1所示的频率分布直方图.

(图1) (图2)
(Ⅰ)求频率分布直方图中字母![]() 的值,并求该组的频率;
的值,并求该组的频率;
(Ⅱ)通过频率分布直方图,估计该市居民每月的用水量的中位数![]() 的值(保留两位小数);
的值(保留两位小数);
(Ⅲ)如图2是该市居民张某2016年1~6月份的月用水费![]() (元)与月份
(元)与月份![]() 的散点图,其拟合的线性回归方程是
的散点图,其拟合的线性回归方程是![]() . 若张某2016年1~7月份水费总支出为312元,试估计张某7月份的用水吨数.
. 若张某2016年1~7月份水费总支出为312元,试估计张某7月份的用水吨数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】宝宝的健康成长是妈妈们最关心的问题,父母亲为婴儿选择什么品牌的奶粉一直以来都是育婴中的一个重要话题,为了解过程奶粉的知名度和消费者的信任度,某调查小组特别调查记录了某大型连锁超市2015年与2016年这两年销售量前5名的五个品牌奶粉的销量(单位:罐),绘制如下的管状图:
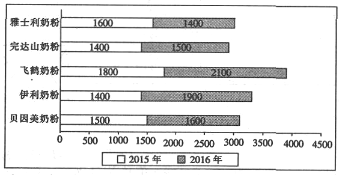
(1)根据给出的这两年销量的管状图,对该超市这两年品牌奶粉销量的前五强进行排名;
(2)分别计算这5个品牌奶粉2016年所占总销量(仅指这5个品牌奶粉的总销量)的百分比(百分数精确到各位),并将数据填入如下饼状图中的括号内;
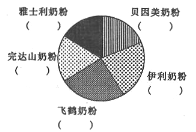
(3)试以(2)中的百分比作为概率,若随机选取2名购买这5个品牌中任意1个品牌的消费者进行采访,记![]() 为被采访中购买飞鹤奶粉的人数,求
为被采访中购买飞鹤奶粉的人数,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4 坐标系与参数方程
在直角坐标系![]() 中,圆
中,圆![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() 为参数),并以
为参数),并以![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)写出![]() 的极坐标方程,并将
的极坐标方程,并将![]() 化为普通方程;
化为普通方程;
(2)若直线![]() 的极坐标方程为
的极坐标方程为![]() 与
与![]() 相交于
相交于![]() 两点,
两点,
求![]() 的面积(
的面积(![]() 为圆
为圆![]() 的圆心).
的圆心).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com