Question

8．给出下列4个命题，其中正确命题的个数是（　　）
①计算：91⁹²除以100的余数是1；
②命题“?x＞0，x-lnx＞0”的否定是“?x＞0，x-lnx≤0”；
③y=tanax（a＞0）在其定义域内是单调函数而且又是奇函数；
④命题p：“|a|+|b|≤1”是命题q：“对任意的x∈R，不等式asinx+bcosx≤1恒成立”的充分不必要条件．

• A． 1个
• B． 2个
• C． 3个
• D． 4个

Answer 1

分析 ①利用二项式定理进行展开判断即可．
②根据含有量词的命题的否定进行判断．
③根据函数单调性和奇偶性的性质进行判断．
④根据充分条件和必要条件的定义结合三角函数的性质进行判断．

解答 解：①由于91⁹²=（100-9）⁹²=C₉₂⁰•100⁹²•（-9）⁰+…+C₉₂⁹¹•100¹•（-9）⁹¹+C₉₂⁹²•100⁰•（-9）⁹²，
在此展开式中，除了最后一项外，其余的项都能被100整除，故91⁹²除以100的余数等价于C₉₂⁹²•100⁰•（-9）⁹²=9⁹²除以100的余数，而9⁹²=（10-1）⁹²=C₉₂⁰•10⁹²•（-1）⁰+…+C₉₂⁹¹•10¹•（-1）⁹¹+C₉₂⁹²•10⁰•（-9）⁹²，故9⁹²除以100的余数等价于C₉₂⁹¹•10¹•（-1）⁹¹+C₉₂⁹²•10⁰•（-9）⁹²除以100的余数，而C₉₂⁹¹•10¹•（-1）⁹¹+C₉₂⁹²•10⁰•（-9）⁹²=-919=-10×100+81，故91⁹²除以100的余数是81．不正确．故①错误；
②命题“?x＞0，x-lnx＞0”的否定是“?x＞0，x-lnx≤0”，正确；
③y=tanax（a＞0）在其定义域内不是单调函数，是奇函数；故③错误，
④当a=b=0时，不等式asinx+bcosx≤1恒成立．
a与b不全为0时，不等式asinx+bcosx≤1化为：sin（x+θ）≤$\frac{1}{\sqrt{{a}^{2}+{b}^{2}}}$，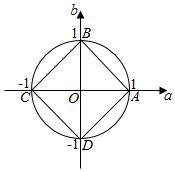
∵对任意的x∈R，不等式asinx+bcosx≤1恒成立”，
∴$\frac{1}{\sqrt{{a}^{2}+{b}^{2}}}$≥1，
∴a²+b²≤1，画出图象：可知：（a，b）表示的是以原点为圆心，1为半径的圆及其内部．
而|a|+|b|≤1可知：（a，b）表示的是正方形ABCD及其内部．
∴p是q的充分不必要条件．故④正确，
故选：B

点评 本题考查命题的真假的判断与应用，考查充要条件，命题的否定，二项式定理，函数单调性和奇偶性的性质，涉及的知识点较多，综合性较强，但难度不大，属于中档题．