
【题目】如图,三棱柱ABC﹣A1B1C1中,∠ACB=90°,CC1⊥底面ABC,AC=BC=CC1=2,D,E,F分别是棱AB,BC,B1C1的中点,G是棱BB1上的动点. 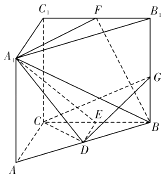
(1)当 ![]() 为何值时,平面CDG⊥平面A1DE?
为何值时,平面CDG⊥平面A1DE?
(2)求平面AB1F与平面AD1E所成的锐二面角的余弦值.
【答案】
(1)解:当G为BB1中点(即 ![]() )时,平面CDG⊥平面A1DE.
)时,平面CDG⊥平面A1DE.
证明如下:由于DE∥AC且 ![]() ,∴
,∴ ![]() ,故D,E,C1,A1四点共面.
,故D,E,C1,A1四点共面.
连接C1E交GC于H.在正方形CBB1C1中, ![]() ,故∠CHE=90°,即CG⊥C1E.又A1C1⊥平面CBB1C1,CG平面CBB1C1,所以DE⊥CG,又因为C1E∩DE=E,故CG⊥平面A1DE,从而平面CDG⊥平面A1DE
,故∠CHE=90°,即CG⊥C1E.又A1C1⊥平面CBB1C1,CG平面CBB1C1,所以DE⊥CG,又因为C1E∩DE=E,故CG⊥平面A1DE,从而平面CDG⊥平面A1DE
(2)解:三棱柱ABC﹣A1B1C1中,∠ACB=90°,CC1⊥底面ABC,
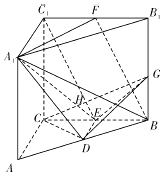
于是可以以C为原点,CA,CB,CC1所在的直线分别为x,y,z轴建立空间直角坐标系,
如图所示.

因为AC=BC=CC1=2,D,E,F分别是棱AB,BC,B1C1的中点,
所以A1(2,0,2),D(1,1,0),E(0,1,0),B(0,2,0),F(0,1,2),
G(0,2.1), ![]() =(﹣2,2,﹣2),
=(﹣2,2,﹣2), ![]() =(﹣2,1,0).
=(﹣2,1,0).
由(1)知平面A1DE的法向量为 ![]() =(0,2,1),
=(0,2,1),
设平面A1BF的法向量为 ![]() =(x,y,z),则
=(x,y,z),则 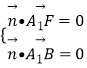 ,即:
,即: ![]() ,
,
令x=1得 ![]() ,
,
设平面A1BF与平面A1DE所成的锐二面角为θ,
则cosθ= ![]() =
= ![]() =
= ![]() .
.
【解析】(1)当G为BB1中点(即 ![]() )时,平面CDG⊥平面A1DE.证明D,E,C1 , A1四点共面.连接C1E交GC于H.证明CG⊥C1E.DE⊥CG,推出CG⊥平面A1DE,即可证明平面CDG⊥平面A1DE.(2)以C为原点,CA,CB,CC1所在的直线分别为x,y,z轴建立空间直角坐标系,求出平面A1DE的法向量,平面A1BF的法向量,设平面A1BF与平面A1DE所成的锐二面角为θ,利用数量积求解即可.
)时,平面CDG⊥平面A1DE.证明D,E,C1 , A1四点共面.连接C1E交GC于H.证明CG⊥C1E.DE⊥CG,推出CG⊥平面A1DE,即可证明平面CDG⊥平面A1DE.(2)以C为原点,CA,CB,CC1所在的直线分别为x,y,z轴建立空间直角坐标系,求出平面A1DE的法向量,平面A1BF的法向量,设平面A1BF与平面A1DE所成的锐二面角为θ,利用数量积求解即可.
【考点精析】本题主要考查了平面与平面垂直的判定的相关知识点,需要掌握一个平面过另一个平面的垂线,则这两个平面垂直才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() 的半径为2,圆心在
的半径为2,圆心在![]() 轴的正半轴上,且与直线
轴的正半轴上,且与直线![]() 相切.
相切.
(1)求圆![]() 的方程。
的方程。
(2)在圆![]() 上,是否存在点
上,是否存在点![]() ,使得直线
,使得直线![]() 与圆
与圆![]() 相交于不同的两点
相交于不同的两点![]() ,且△
,且△![]() 的面积最大?若存在,求出点
的面积最大?若存在,求出点![]() 的坐标及对应的△
的坐标及对应的△![]() 的面积;若不存在,请说明理由.
的面积;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知点
中,已知点![]() 为直线
为直线![]() 上一点,过点
上一点,过点![]() 作
作![]() 的垂线与以
的垂线与以![]() 为直径的圆
为直径的圆![]() 相交于
相交于![]() ,
,![]() 两点.
两点.
(1)若![]() ,求圆
,求圆![]() 的方程;
的方程;
(2)求证:点![]() 始终在某定圆上.
始终在某定圆上.
(3)是否存在一定点![]() (异于点
(异于点![]() ),使得
),使得![]() 为常数?若存在,求出定点
为常数?若存在,求出定点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数 ![]() ,则关于函数f(x)有以下四个命题( )
,则关于函数f(x)有以下四个命题( )
①x∈R,f(f(x))=1;
②x0 , y0∈R,f(x0+y0)=f(x0)+f(y0);
③函数f(x)是偶函数;
④函数f(x)是周期函数.
其中真命题的个数是( )
A.4
B.3
C.2
D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=2x﹣a,g(x)=x+2.
(1)当a=1时,求不等式f(x)+f(﹣x)≤g(x)的解集;
(2)求证: ![]() 中至少有一个不小于
中至少有一个不小于 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cos(ωx+φ)(ω>0),f'(x)是f(x)的导函数,若f(α)=0,f'(α)>0,且f(x)在区间[α, ![]() +α)上没有最小值,则ω取值范围是( )
+α)上没有最小值,则ω取值范围是( )
A.(0,2)
B.(0,3]
C.(2,3]
D.(2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据统计,某地区植被覆盖面积![]() 公顷
公顷![]() 与当地气温下降的度数
与当地气温下降的度数![]() 之间呈线性相关关系,对应数据如下:
之间呈线性相关关系,对应数据如下:
| 20 | 40 | 60 | 80 |
| 3 | 4 | 4 | 5 |
![]() 请用最小二乘法求出y关于x的线性回归方程;
请用最小二乘法求出y关于x的线性回归方程;
![]() 根据
根据![]() 中所求线性回归方程,如果植被覆盖面积为300公顷,那么下降的气温大约是多少
中所求线性回归方程,如果植被覆盖面积为300公顷,那么下降的气温大约是多少![]() ?
?
参考公式:线性回归方程![]() ;其中
;其中![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com