
 如图,在直三棱柱ABC-A1B1C1中,D是BC上的一点,AB=AC,且AD⊥BC
如图,在直三棱柱ABC-A1B1C1中,D是BC上的一点,AB=AC,且AD⊥BC分析 (1)连接A1B交AB1于E,连接DE,根据中位线定理即可得出DE∥A1C,故而A1C∥平面AB1D1;
(2)过B作BF⊥B1D,则可证BF⊥平面AB1D,于是点A1到平面AB1D的距离等于C到平面AB1D的距离,等于B到平面AB1D的距离BF.
解答  证明:(1)连接A1B交AB1于E,连接DE,
证明:(1)连接A1B交AB1于E,连接DE,
∵四边形ABB1A1是平行四边形,
∴E是AB1的中点,
∵AB=AC,AD⊥BC,
∴D是BC的中点,
∴DE∥A1C,
又DE?平面AB1D,A1C?平面AB1D,
∴A1C∥平面AB1D1.
(2)∵A1C∥平面AB1D1,
∴A1到平面AB1D的距离等于C到平面AB1D的距离,
∵D是BC的中点,
∴C到平面AB1D的距离等于B到平面AB1D的距离,
过B作BF⊥B1D于F,
∵BB1⊥平面ABC,AD?平面ABC,
∴AD⊥BB1,
又∵AD⊥BC,BB1∩BC=B,
∴AD⊥平面BCC1B1,
∴AD⊥BF,又B1D∩AD=D,
∴BF⊥平面AB1D,即BF为B到平面AB1D的距离,
∵BD=1,BB1=2,∴B1D=$\sqrt{5}$,
∴BF=$\frac{BD•B{B}_{1}}{{B}_{1}D}$=$\frac{2\sqrt{5}}{5}$.
∴A1到平面AB1D的距离为$\frac{2\sqrt{5}}{5}$.
点评 本题考查了线面平行的判定,线面距离的计算,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 某几何体的三视图如图所示,其中俯视图是半圆里面内切一个小圆,若该几何体的表面积为16+16π,则正视图中的a值为( )
某几何体的三视图如图所示,其中俯视图是半圆里面内切一个小圆,若该几何体的表面积为16+16π,则正视图中的a值为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 有一塔形几何体由若干个正方体构成,构成方式如图所示,上层正方体下底面的四个顶点是下层正方体上底面各边的中点.已知最底层正方体的棱长为2,且该塔形的表面积(含最底层正方体的底面面积)超过38,则该塔形中正方体的个数至少是( )
有一塔形几何体由若干个正方体构成,构成方式如图所示,上层正方体下底面的四个顶点是下层正方体上底面各边的中点.已知最底层正方体的棱长为2,且该塔形的表面积(含最底层正方体的底面面积)超过38,则该塔形中正方体的个数至少是( )| A. | 4个 | B. | 5个 | C. | 6个 | D. | 7个 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
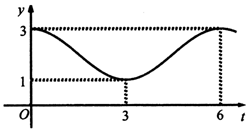 某工厂有甲、乙两生产车间,其污水瞬时排放量y(单位:m3/h )关于时间t(单位:h)的关系均近似地满足函数y=Asin(ωt+φ)+b(A>0,ω>0,0<φ<π),其图象如下:
某工厂有甲、乙两生产车间,其污水瞬时排放量y(单位:m3/h )关于时间t(单位:h)的关系均近似地满足函数y=Asin(ωt+φ)+b(A>0,ω>0,0<φ<π),其图象如下:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 40 | B. | 41 | C. | 82 | D. | 83 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com