
分析 (1)利用圆心到直线的距离公式求圆的半径,从而求解圆的方程;
(2)根据相交弦长公式,求出圆心到直线的距离,设出直线方程,再根据点到直线的距离公式确定直线方程.
解答 解:(1)设圆A的半径为r,∵圆A与直线l1:x+2y+7=0相切,
∴$r=\frac{{|{-1+4+7}|}}{{\sqrt{5}}}=2\sqrt{5}$,∴圆A的方程为(x+1)2+(y-2)2=20.
(2)当直线l与x轴垂直时,易知直线l的方程为x=-4,
此时$|{MN}|=2\sqrt{11}$,符合题意;
当直线l与x轴不垂直时,设直线l的斜率为k,
则直线l的方程为y=k(x+4),即kx-y+4k=0,
设MN的中点为Q,则AQ⊥MN,
∴${|{AQ}|^2}+(\frac{1}{2}{|{MN}|^2})={r^2}$,又$|{MN}|=2\sqrt{11}$,$r=2\sqrt{5}$,
∴$AQ=\sqrt{20-11}=3$,又$|{AQ}|=\frac{{|{-k-2+4k}|}}{{\sqrt{{k^2}+1}}}$,∴$\frac{{|{-k-2+4k}|}}{{\sqrt{{k^2}+1}}}=3⇒k=-\frac{5}{12}$,
则直线l的方程为:$y=-\frac{5}{12}(x+4)$,即5x+12y+20=0,
综上可知直线l的方程为:x=-4或5x+12y+20=0.
点评 本题考查圆的标准方程及直线与圆的相交弦长问题,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3π | B. | 4π | C. | 5π | D. | 6π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
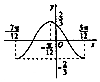 函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则f($\frac{π}{12}$)=( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则f($\frac{π}{12}$)=( )| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{2}}{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p | B. | ¬q | C. | p∧q | D. | p∨q |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com