
| A. | {-$\frac{π}{5}$,$\frac{3π}{10}$} | B. | {-$\frac{7π}{10}$,$\frac{4π}{5}$} | ||
| C. | {-$\frac{π}{5}$,-$\frac{7π}{10}$,$\frac{3π}{10}$,$\frac{4π}{5}$} | D. | {$\frac{3π}{10}$,-$\frac{7π}{10}$} |
分析 只要解-π<$\frac{kπ}{2}$-$\frac{π}{5}$<π,对k取值即可.
解答 解:由题意-π<$\frac{kπ}{2}$-$\frac{π}{5}$<π,解得-$\frac{8}{5}$<k<$\frac{12}{5}$,又k∈Z,所以k=-1,0,1,2,
所以集合{α|α=$\frac{kπ}{2}$-$\frac{π}{5}$,k∈Z}∩{α|-π<α<π}={-$\frac{π}{5}$,-$\frac{7π}{10}$,$\frac{3π}{10}$,$\frac{4π}{5}$}
故选:C.
点评 本题考查了集合的运算,关键是确定k的取值,属于基础题.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案科目:高中数学 来源: 题型:解答题
| 生二胎 | 不生二胎 | 合计 | |
| 70后 | 30 | 15 | 45 |
| 80后 | 45 | 10 | 55 |
| 合计 | 75 | 25 | 100 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=±$\frac{a}{2}$x | B. | y=±$\frac{\sqrt{3}}{2}$x | C. | y=±$\frac{\sqrt{3}}{3}$x | D. | y=±$\sqrt{3}$x |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
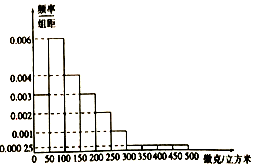 根据环境保护部《环境空气质量指数(AQI)技术规定》,空气质量指数(AQI)在201-300之间为重度污染;在301-500之间为严重污染.依据空气质量预报,同时综合考虑空气污染程度和持续时间,将空气重污染分4个预警级别,由轻到重依次为预警四级、预警三级、预警二级、预警一级,分别用蓝、黄、橙、红颜色标示,预警一级(红色)为最高级别.(一)预警四级(蓝色):预测未来1天出现重度污染;(二)预警三级(黄色):预测未来1天出现严重污染或持续3天出现重度污染;(三)预警二级(橙色);预测未来持续3天交替出现重度污染或严重污染;(四)预警一级(红色);预测未来持续3天出现严重污染.
根据环境保护部《环境空气质量指数(AQI)技术规定》,空气质量指数(AQI)在201-300之间为重度污染;在301-500之间为严重污染.依据空气质量预报,同时综合考虑空气污染程度和持续时间,将空气重污染分4个预警级别,由轻到重依次为预警四级、预警三级、预警二级、预警一级,分别用蓝、黄、橙、红颜色标示,预警一级(红色)为最高级别.(一)预警四级(蓝色):预测未来1天出现重度污染;(二)预警三级(黄色):预测未来1天出现严重污染或持续3天出现重度污染;(三)预警二级(橙色);预测未来持续3天交替出现重度污染或严重污染;(四)预警一级(红色);预测未来持续3天出现严重污染.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com