
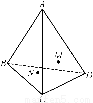
在四面体ABCD中,M、N分别是平面△ACD、△BCD的重心,则四面体的四个面中与MN平行的是________.
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第八章第5课时练习卷(解析版) 题型:解答题
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,点E在线段AD上,且CE∥AB.
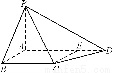
(1)求证:CE⊥平面PAD;
(2)若PA=AB=1,AD=3,CD= ,∠CDA=45°,求四棱锥P-ABCD的体积.
,∠CDA=45°,求四棱锥P-ABCD的体积.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第八章第3课时练习卷(解析版) 题型:解答题
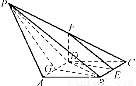
如图,在锥体PABCD中,ABCD是边长为1的菱形,且∠DAB=60°,PA=PD=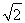 ,PB=2,E、F分别是BC、PC的中点.证明:AD⊥平面DEF.
,PB=2,E、F分别是BC、PC的中点.证明:AD⊥平面DEF.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第八章第2课时练习卷(解析版) 题型:解答题
正三棱柱ABCA1B1C1中,已知AB=A1A,D为C1C的中点,O为A1B与AB1的交点.
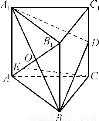
(1)求证:AB1⊥平面A1BD;
(2)若点E为AO的中点,求证:EC∥平面A1BD.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第八章第2课时练习卷(解析版) 题型:解答题
如图,四边形ABCD为正方形,在四边形ADPQ中,PD∥QA.又QA⊥平面ABCD,QA=AB=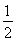 PD.
PD.
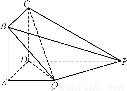
(1)证明:PQ⊥平面DCQ;
(2)CP上是否存在一点R,使QR∥平面ABCD,若存在,请求出R的位置,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第八章第1课时练习卷(解析版) 题型:解答题
如图,在四面体ABCD中作截面PQR,若PQ、CB的延长线交于M,RQ、DB的延长线交于N,RP、DC的延长线交于K.
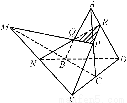
求证:M、N、K三点共线.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第八章第1课时练习卷(解析版) 题型:解答题
已知A是△BCD平面外的一点,E,F分别是BC,AD的中点.
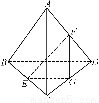
(1)求证:直线EF与BD是异面直线;
(2)若AC⊥BD,AC=BD,求EF与BD所成的角.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第五章第6课时练习卷(解析版) 题型:解答题
正项数列{an}的前项和满足: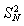 -(n2+n-1)Sn-(n2+n)=0.
-(n2+n-1)Sn-(n2+n)=0.
(1)求数列{an}的通项公式an;
(2)令bn=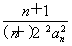 ,数列{bn}的前n项和为Tn.证明:对于任意的n∈N*,都有Tn<
,数列{bn}的前n项和为Tn.证明:对于任意的n∈N*,都有Tn<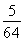 .
.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第五章第4课时练习卷(解析版) 题型:填空题
已知数列{an}中,a1=1,(n+1)an+1=nan(n∈N*),则该数列的通项公式an=________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com