
【题目】如图,已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,以线段
,以线段![]() 为直径的圆与椭圆交于点
为直径的圆与椭圆交于点 .
.

(1)求椭圆的方程;
(2)过![]() 轴正半轴上一点
轴正半轴上一点![]() 作斜率为
作斜率为![]() 的直线
的直线![]() .
.
①若![]() 与圆和椭圆都相切,求实数
与圆和椭圆都相切,求实数![]() 的值;
的值;
②直线![]() 在
在![]() 轴左侧交圆于
轴左侧交圆于![]() 、
、![]() 两点,与椭圆交于点
两点,与椭圆交于点![]() 、
、![]() (从上到下依次为
(从上到下依次为![]() 、
、![]() 、
、![]() 、
、![]() ),且
),且![]() ,求实数
,求实数![]() 的最大值.
的最大值.
【答案】(1)![]() (2)①
(2)①![]() ②
②![]() 的最大值为3
的最大值为3
【解析】
(1)线段![]() 为直径的圆与椭圆交于点
为直径的圆与椭圆交于点![]() ,可以得圆的方程及
,可以得圆的方程及![]() ,将点
,将点![]() 代入椭圆方程得
代入椭圆方程得![]() ,又因为
,又因为![]() ,就可解出
,就可解出![]() ,
,![]() ,进而得出椭圆方程.
,进而得出椭圆方程.
(2)①设直线![]() 的方程为:
的方程为:![]() ,即
,即![]() ,因为
,因为![]() 与圆和椭圆相切,得
与圆和椭圆相切,得![]() ,△
,△![]() ,解得,
,解得,![]() ,
,![]() .
.
②取![]() 中点
中点![]() ,连接
,连接![]() ,则
,则![]() ,又
,又![]() ,所以点
,所以点![]() 为
为![]() 中点,写出
中点,写出![]() 点坐标,进而得
点坐标,进而得![]() 坐标,代入椭圆方程化简得,
坐标,代入椭圆方程化简得,![]() ,设
,设![]() ,最后再求则
,最后再求则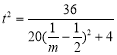 最值.
最值.
解:(1)设椭圆的焦距为![]()
因为线段![]() 为直径的圆与椭圆交于点
为直径的圆与椭圆交于点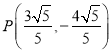
所以![]()
又点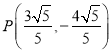 在椭圆上
在椭圆上
所以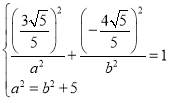 ,解得
,解得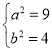
所以椭圆的方程为![]()
(2)①因为直线![]() 与圆相切,所以
与圆相切,所以![]() ,即
,即![]() (ⅰ)
(ⅰ)
由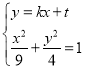 ,消去
,消去![]() 得
得![]()
因为直线与椭圆相切,
所以![]() 即
即![]() (ⅱ)
(ⅱ)
联立(i)(ⅱ)得![]() 负值舍去
负值舍去
②取![]() 中点
中点![]() ,连结
,连结![]() ,则
,则![]() ,
,
又![]() ,所以
,所以![]() 为
为![]() 中点
中点
由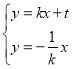 ,解得
,解得![]()
所以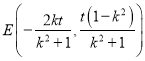
代入椭圆方程化简得
设![]()
则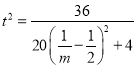 ,当
,当![]() 时,
时,![]() 取最大值3,此时
取最大值3,此时![]() .
.
又![]() ,
,![]() 时,
时,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
符合题意,故![]() 的最大值为3.
的最大值为3.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() 在区间
在区间![]() 上的最大值为9,最小值为1,记
上的最大值为9,最小值为1,记![]()
(1)求实数![]() ,
,![]() 的值;
的值;
(2)若不等式![]() 成立,求实数
成立,求实数![]() 的取值范围;
的取值范围;
(3)定义在![]() 上的函数
上的函数![]() ,设
,设![]() ,
,![]() 将区间
将区间![]() 任意划分成
任意划分成![]() 个小区间,如果存在一个常数
个小区间,如果存在一个常数![]() ,使得和式
,使得和式![]() 恒成立,则称函数
恒成立,则称函数![]() 为在
为在![]() 上的有界变差函数.试判断函数
上的有界变差函数.试判断函数![]() 是否为在
是否为在![]() 上的有界变差函数?若是,求
上的有界变差函数?若是,求![]() 的最小值;若不是,请说明理由(
的最小值;若不是,请说明理由(![]() 表示
表示![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)是定义域为R的偶函数,且f(x+3)=f(x-1),若当x∈[-2,0]时,f(x)=2-x,记![]() ,
,![]() ,c=f(32),则a,b,c的大小关系为( )
,c=f(32),则a,b,c的大小关系为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
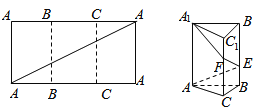
【题目】如图,把长为6,宽为3的矩形折成正三棱柱![]() ,三棱柱的高度为3,矩形的对角线和三棱柱的侧棱
,三棱柱的高度为3,矩形的对角线和三棱柱的侧棱![]() 的交点记为E,F.
的交点记为E,F.
(1)求三棱柱![]() 的体积;
的体积;
(2)求三棱柱中异面直线![]() 与
与![]() 所成角的大小.
所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
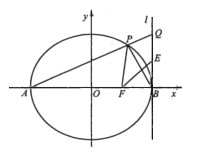
【题目】在平面直角坐标系xOy中,已知椭圆C:![]() 的左、右顶点为A,B,右焦点为F.过点A且斜率为k(
的左、右顶点为A,B,右焦点为F.过点A且斜率为k(![]() )的直线交椭圆C于另一点P.
)的直线交椭圆C于另一点P.
(1)求椭圆C的离心率;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)设直线l:![]() ,延长AP交直线l于点Q,线段BQ的中点为E,求证:点B关于直线EF的对称点在直线PF上.
,延长AP交直线l于点Q,线段BQ的中点为E,求证:点B关于直线EF的对称点在直线PF上.
查看答案和解析>>
科目:高中数学 来源: 题型:
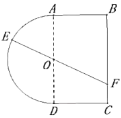
【题目】一个玩具盘由一个直径为2米的半圆O和一个矩形ABCD构成,![]() 米,如图所示.小球从A点出发以5 V的速度沿半圆O轨道滚到某点E处后,经弹射器以6 V的速度沿与点E切线垂直的方向弹射到落袋区BC内,落点记为F.设
米,如图所示.小球从A点出发以5 V的速度沿半圆O轨道滚到某点E处后,经弹射器以6 V的速度沿与点E切线垂直的方向弹射到落袋区BC内,落点记为F.设![]() 弧度,小球从A到F所需时间为T.
弧度,小球从A到F所需时间为T.
(1)试将T表示为![]() 的函数
的函数![]() ,并写出定义域;
,并写出定义域;
(2)当![]() 满足什么条件时,时间T最短.
满足什么条件时,时间T最短.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某文体局为了解“跑团”每月跑步的平均里程,收集并整理了2018年1月至2018年11月期间“跑团”每月跑步的平均里程(单位:公里)的数据,绘制了下面的折线图.根据折线图,下列结论正确的是( )

A. 月跑步平均里程的中位数为6月份对应的里程数
B. 月跑步平均里程逐月增加
C. 月跑步平均里程高峰期大致在8、9月
D. 1月至5月的月跑步平均里程相对于6月至11月,波动性更小,变化比较平稳
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的前
的前![]() 项和为
项和为![]() ,若
,若![]() ,则称
,则称![]() 是“紧密数列”.
是“紧密数列”.
(1)若数列![]() 是“紧密数列”,且
是“紧密数列”,且![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 的取值范围;
的取值范围;
(2)若![]() 为等差数列,首项
为等差数列,首项![]() ,公差
,公差![]() ,且
,且![]() ,判断
,判断![]() 是否为“紧密数列”,并说明理由;
是否为“紧密数列”,并说明理由;
(3)设数列![]() 是公比为
是公比为![]() 的等比数列,若数列
的等比数列,若数列![]() 与
与![]() 都是“紧密数列”,求
都是“紧密数列”,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com