已知数列{an} 和{bn} 的通项分别为an=2n-1,bn=2n+1-1(n∈N*),集合A={x|x=an,n∈N*},B={x|x=bn,n∈N*},设D=CAB.将集合D中元素从小到大依次排列,构成数列d1,d2,d3,…,dn,….
(1)写出d1,d2,d3,d4;
(2)求数列{dn}的前2012项的和;
(3)是否存在这样的无穷等差数列{cn}:使得Cn∈D(n∈N*)?若存在,请写出一个这样的数列,并加以证明;若不存在,请说明理由.
【答案】
分析:(1)根据数列的通项,写出相应的项,由此可写出d
1,d
2,d
3,d
4;
(2)数列{d
n}的前2012项的和为数列{a
n}的前2012项的和减去{b
n}的前10项的和,由此可得结论
(3)存在,列举一个c
n=6n-1=2×3n-1,n∈N
*,证明c
n∈A,c
n∉B即可.
解答:解:(1)∵a
n=2n-1,b
n=2
n+1-1,
∴a
1=1,b
1=3;a
2=3,b
2=7;a
3=5,b
3=15;
∴A={1,3,5,7,9,11,13,…2n-1},B={3,7,15,31,63,127,…2
n+1-1},
∵D=C
AB,集合D中元素从小到大依次排列,构成数列d
1,d
2,d
3,…,d
n,….
∴d
1=1,d
2=5,d
3=9,d
4=11;
(2)b
1=3,b
2=7,b
3=15,…b
10=2047,b
11=4095,a
2012=2×2012-1=4023,a
2022=2n-1=4043
∴数列{d
n}的前2012项的和为a
1+a
2+…+a
2012-(b
1+b
2+…+b
10)=2022
2-(2
12-14)=40402
(3)存在.如c
n=6n-1(n∈N
*),
证明:c
n=6n-1=2×3n-1,n∈N
*,所以3n∈N
*,所以c
n∈A
假设c
n∈B,则存在实数k,6n-1=2
k+1-1,所以n=
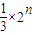
(n∈N
*),
由于上式左边为整数,右边为分数,所以上式不成立,所以假设不成立,所以c
n∉B
所以c
n∈D.即c
n=6n-1(n∈N
*)满足要求.
点评:本题考查数列知识的综合,考查数量的通项与求和,解题的关键是理解数列的新定义,有难度.

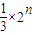 (n∈N*),
(n∈N*),
