
【题目】已知双曲线 ![]() ﹣
﹣ ![]() =1(a>0,b>0)的左、右焦点分别为F1、F2 , 点P(x0 ,
=1(a>0,b>0)的左、右焦点分别为F1、F2 , 点P(x0 , ![]() )为双曲线上一点,若△PF1F2的内切圆半径为1,且圆心G到原点O的距离为
)为双曲线上一点,若△PF1F2的内切圆半径为1,且圆心G到原点O的距离为 ![]() ,则双曲线的离心率是 .
,则双曲线的离心率是 .
【答案】![]()
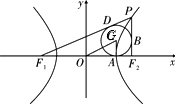
【解析】解:设P为第一象限的点,
圆与F1F2,PF1,PF2的切点分别为A',B,D.
∵|PF1|﹣|PF2|=2a,|PD|=|PB|,|DF1|=|A'F1|,|BF2|=|A'F2|,
即为|PD|+|DF1|﹣|PB|﹣|BF2|=|DF1|﹣|BF2|=|A'F1|﹣|A'F2|=2a,
且|A'F1|+|A'F2|=2c,可得|A'F2|=c﹣a,
则A与A'重合,则|OA'|=|OA|=a,
故 ![]() =
= ![]() ,即a=2.
,即a=2.
又△PF1F2的面积S= ![]() ×
× ![]() ×|2c|=
×|2c|= ![]() (|F1F2|+|PF1|+|PF2|)×1,
(|F1F2|+|PF1|+|PF2|)×1,
∴|PF1|+|PF2|=3c,
∵|PF1|﹣|PF2|=2a,
∴|PF1|= ![]() ,|PF2|=
,|PF2|= ![]() ,
,
∵|PF1|= ![]() ,|PF2|=
,|PF2|= ![]() ,联立化简得x0=3.
,联立化简得x0=3.
P代入双曲线方程,联立解得b= ![]() ,c=
,c= ![]() =3,
=3,
即有双曲线的离心率为e= ![]() =
= ![]() .
.
所以答案是: ![]() .
.


 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:高中数学 来源: 题型:
【题目】如图,已知直角梯形ACDE所在的平面垂直于平面ABC,∠BAC=
∠ACD=90°,∠EAC=60°,AB=AC=AE.
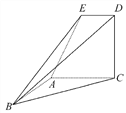
(1)在直线BC上是否存在一点P,使得DP∥平面EAB?请证明你的结论.
(2)求平面EBD与平面ABC所成的锐二面角θ的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC中,A(0,1),AB边上的高CD所在直线的方程为x+2y-4=0,AC边上的中线BE所在直线的方程为2x+y-3=0.
(1)求直线AB的方程;
(2)求直线BC的方程;
(3)求△BDE的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了保护学生的视力,教室内的日光灯在使用一段时间后必须更换.已知某校使用的100只日光灯在必须换掉前的使用天数如下表:
天数/天 | 151~180 | 181~210 | 211~240 | 241~270 | 271~300 | 301~330 | 331~360 | 361~390 |
灯管数/只 | 1 | 11 | 18 | 20 | 25 | 16 | 7 | 2 |
(1)试估计这种日光灯的平均使用寿命;
(2)若定期更换,可选择多长时间统一更换合适?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在底面为平行四边形的四棱锥P﹣ABCD中,PA⊥平面ABCD,且BC=2AB═4,∠ABC=60°,点E是PD的中点. 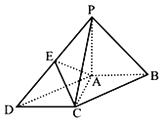
(1)求证:AC⊥PB;
(2)当二面角E﹣AC﹣D的大小为45°时,求AP的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>0)的焦点在x轴上,且椭圆C的焦距为2. (Ⅰ)求椭圆C的标准方程;
=1(a>0)的焦点在x轴上,且椭圆C的焦距为2. (Ⅰ)求椭圆C的标准方程;
(Ⅱ)过点R(4,0)的直线l与椭圆C交于两点P,Q,过P作PN⊥x轴且与椭圆C交于另一点N,F为椭圆C的右焦点,求证:三点N,F,Q在同一条直线上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,PA⊥AB,PA⊥BC,AB=BC,D为线段AC的中点.

(1)求证:PA⊥BD.
(2)求证:BD⊥平面PAC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com