
【题目】如图,在四棱锥P-ABCD 中,AB∥CD ,AB⊥AD,CD=2AB,平面PAD⊥底面ABCD,PA⊥AD,E和F分别为CD和PC的中点.求证:
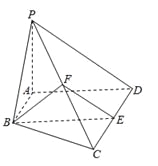
(1)BE∥平面PAD;
(2)平面BEF⊥平面PCD.
【答案】详见解析
【解析】试题分析:(1)根据条件,易证四边形![]() 是平行四边形,所以
是平行四边形,所以![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ;
;
(2)由条件易证![]() 平面
平面![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() ,
,![]() ,根据中点,
,根据中点,![]() ,所以
,所以![]() ,
,![]() ,那么可证明
,那么可证明![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,根据面面垂直的判定定理,平面
,根据面面垂直的判定定理,平面![]() 平面
平面![]() .
.
试题解析:证明:(1)因为平面PAD⊥底面ABCD,且PA垂直于这两个平面的交线AD,所以PA⊥底面ABCD.
因为AB∥CD,CD=2AB,E为CD的中点,所以AB∥DE,且AB=DE.
所以ABED为平行四边形,所以BE∥AD.
又因为![]() 平面PAD,AD
平面PAD,AD![]() 平面PAD,所以BE∥平面PAD.
平面PAD,所以BE∥平面PAD.
(2)因为AB⊥AD,而且ABED为平行四边形,所以BE⊥CD,AD⊥CD.
由(1)知PA⊥底面ABCD,所以PA⊥CD,因为PA![]() AD=A,
AD=A,
所以CD⊥平面PAD,所以CD⊥PD.
因为E和F分别是CD和PC的中点,所以PD∥EF,所以CD⊥EF.
又EF![]() BE=E,所以CD⊥平面BEF.
BE=E,所以CD⊥平面BEF.
所以平面BEF⊥平面PCD.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某校100名学生期中考试数学成绩的频率分布直方图如图,其中成绩分组区间如下:
组号 | 第一组 | 第二组 | 第三组 | 第四组 | 第五组 |
分组 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
(1)求图中a的值;
(2)根据频率分布直方图,估计这100名学生期中考试数学成绩的平均分;
(3)现用分层抽样的方法从第3、4、5组中随机抽取6名学生,将该样本看成一个总体,从中随机抽取2名,求其中恰有1人的分数不低于90分的概率?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂修建一个长方体无盖蓄水池,其容积为6400立方米,深度为4米.池底每平方米的造价为120元,池壁每平方米的造价为100元.设池底长方形的长为x米.
(Ⅰ)求底面积,并用含x的表达式表示池壁面积;
(Ⅱ)怎样设计水池能使总造价最低?最低造价是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在棱长为1的正方体ABCD—A1B1C1D1中,
M、N分别是AB1、BC1的中点.
(Ⅰ)求证:直线MN//平面ABCD.
(Ⅱ)求B1到平面A1BC1的距离.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空间中任意放置的棱长为2的正四面体![]() .下列命题正确的是_________.(写出所有正确的命题的编号)
.下列命题正确的是_________.(写出所有正确的命题的编号)
①正四面体![]() 的主视图面积可能是
的主视图面积可能是![]() ;
;
②正四面体![]() 的主视图面积可能是
的主视图面积可能是![]() ;
;
③正四面体![]() 的主视图面积可能是
的主视图面积可能是![]() ;
;
④正四面体![]() 的主视图面积可能是2
的主视图面积可能是2
⑤正四面体![]() 的主视图面积可能是
的主视图面积可能是![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面为平行四边形,PD⊥平面ABCD,M为PC中点.
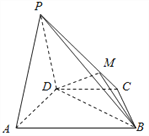
(1)求证:AP∥平面MBD;
(2)若AD⊥PB,求证:BD⊥平面PAD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com