练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设二次函数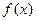满足：（1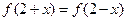），（2）被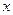轴截得的弦长为2，（3）在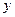轴截距为6，求此函数解析式。

    解：根据题意可知函数对称轴为，由被轴截得的弦长为2，可得的两根，，可设，由，∴

    解析

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    已知函数.
    （1）求的值域G；
    （2）若对于G内的所有实数，不等式恒成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （本小题满分14分）设二次函数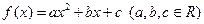满足下列条件：
    ①当∈R时，的最小值为0，且f (－1)=f(－－1)成立；
    ②当∈(0,5)时，≤≤2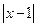+1恒成立。
    （1）求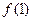的值；    
    （2）求的解析式；
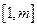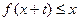    （3）求最大的实数m(m>1),使得存在实数t,只要当∈时，就有成立。

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知函数是定义在上的奇函数,当时，.
    (1)求函数的解析式；并判断在上的单调性(不要求证明)；
    (2)解不等式.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （本小题满分13分）
    某出版公司为一本畅销书定价如下: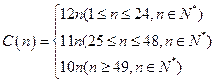.这里n表示定购书
    的数量,C（n）是定购n本书所付的钱数（单位:元）
    （1）有多少个n,会出现买多于n本书比恰好买n本书所花钱少?
    （2）若一本书的成本价是5元,现有两人来买书,每人至少买1本,两人共买60本,问出版公司至少能赚多少钱?最多能赚多少钱?

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （本小题满分12分）
    （1）判断函数的奇偶性；
    （2）若，求a的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （本小题满分12分）
    设二次函数在区间上的最大值、最小值分别是M、m，集合．
    （1）若，且，求M和m的值；
    （2）若，且，记，求的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    .定义在上的函数满足：则不等式（其中 
    为自然对数的底数）的解集为（ ）

    A．B．
    C．D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    (本题12分)已知不等式的解集为；
    (1)求的值；
    (2)若不等式在上恒成立，求实数的最大值.

    查看答案和解析>>

    同步练习册答案